Problem:
Three points are chosen randomly and independently on a circle. What is the probability that all three pairwise distances between the points are less than the radius of the circle?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
We can assume that the circle has its center at and a radius of 1 . Call the three points , and , and let , and denote the length of the counterclockwise arc from to , and , respectively. Rotating the circle if necessary, we can also assume that . Since and are chosen at random from , the ordered pair is chosen at random from a square with area in the -plane. The condition of the problem is met if and only if
This last inequality is equivalent to .
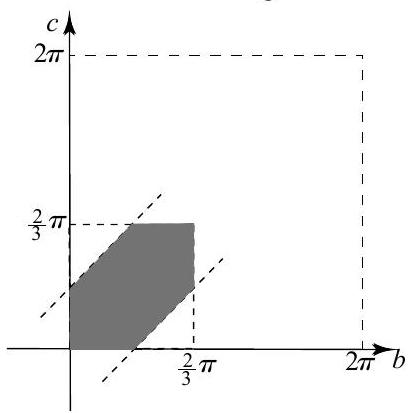
The graph of the common solution to these inequalities is the shaded region shown. The area of this region is
so the requested probability is
The problems on this page are the property of the MAA's American Mathematics Competitions