Problem:
Andrea inscribed a circle inside a regular pentagon, circumscribed a circle around the pentagon, and calculated the area of the region between the two circles. Bethany did the same with a regular heptagon (7 sides). The areas of the two regions were and , respectively. Each polygon had a side length of 2 . Which of the following is true?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
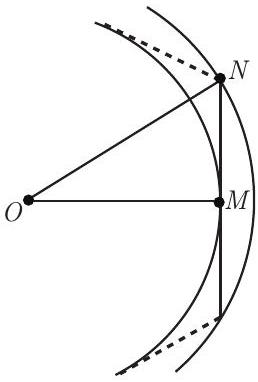
Consider a regular -gon with side length 2. Let the radii of its inscribed and circumscribed circles be and , respectively. Let be the common center of the circles, let be the midpoint of one side of the polygon, and let be one endpoint of that side. Then has a right angle at , and . By the Pythagorean Theorem, . Thus the area of the annulus between the circles is for all . Hence .
The problems on this page are the property of the MAA's American Mathematics Competitions