Problem:
In the -plane, a circle of radius with center on the positive axis is tangent to the -axis at the origin, and a circle of radius with center on the positive -axis is tangent to the -axis at the origin. What is the slope of the line passing through the two points at which these circles intersect?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
In rectangular coordinates, the equations of the circles are and , respectively. Subtracting the two equations and simplifying yields . Any point lying on both circles must satisfy this equation, which must therefore be the equation of the line through the two points of intersection. The requested slope is . The second intersection point can be found by solving the system of equations, and this point is .
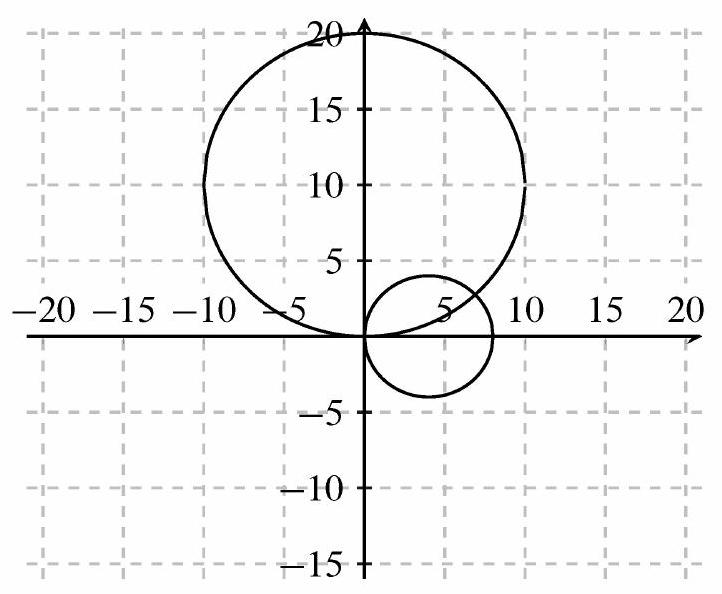
In polar coordinates, the equations of the circles are and , respectively. The circles intersect at the origin and at the point where . In the second case, this equation implies that . The requested slope is therefore .
Let and be the centers of the two circles, and let and be their intersection points. Because and , the diagonals of kite are perpendicular. The slope of is , and the slope of is the negative reciprocal of this value, namely .
The problems on this page are the property of the MAA's American Mathematics Competitions