Problem:
A function f has domain [0,2] and range [0,1]. (The notation [a,b] denotes {x:a≤x≤b}.) What are the domain and range, respectively, of the function g defined by g(x)=1−f(x+1)?
Answer Choices:
A. [−1,1],[−1,0]
B. [−1,1],[0,1]
C. [0,2],[−1,0]
D. [1,3],[−1,0]
E. [1,3],[0,1]
Solution:
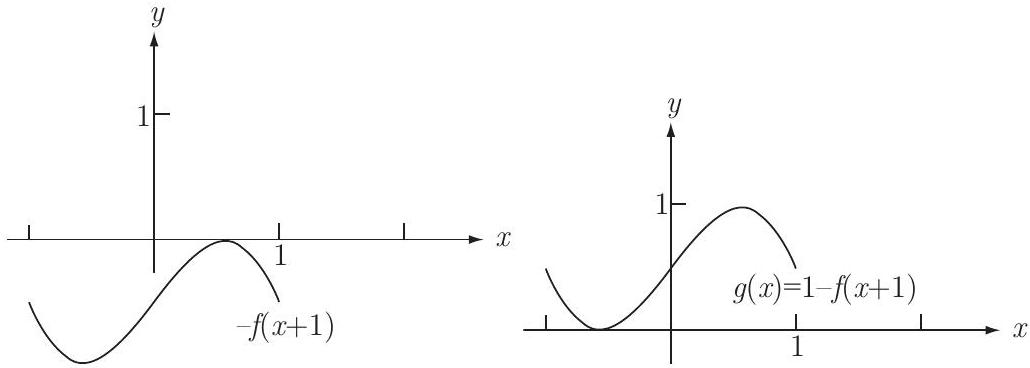
Because the domain of f is [0,2],f(x+1) is defined for 0≤x+1≤2, or −1≤x≤1. Thus g(x) is also defined for −1≤x≤1, so its domain is [−1,1]​. Because the range of f is [0,1], the values of f(x+1) are all the numbers between 0 and 1 , inclusive. Thus the values of g(x) are all the numbers between 1−0=1 and 1−1=0, inclusive, so the range of g is [0,1]​.
OR
The graph of y=f(x+1) is obtained by shifting the graph of y=f(x) one unit to the left. The graph of y=−f(x+1) is obtained by reflecting the graph of y=f(x+1) across the x-axis. The graph of y=g(x)=1−f(x+1) is obtained by shifting the graph of y=−f(x+1) up one unit. As the figures illustrate, the domain and range of g are [−1,1] and [0,1], respectively.\
The problems on this page are the property of the MAA's American Mathematics Competitions
.jpg)
