Problem:
A point is randomly selected from the rectangular region with vertices , . What is the probability that is closer to the origin than it is to the point ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
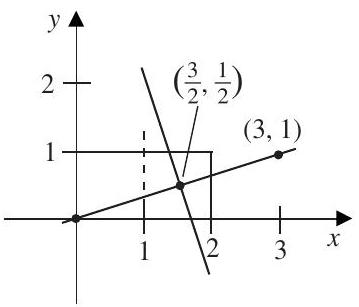
The area of the rectangular region is 2 . Hence the probability that is closer to than it is to is half the area of the trapezoid bounded by the lines , the - and -axes, and the perpendicular bisector of the segment joining and . The perpendicular bisector goes through the point , which is the center of the square whose vertices are , and Hence, the line cuts the square into two quadrilaterals of equal area . Thus the area of the trapezoid is and the probability is .
The problems on this page are the property of the MAA's American Mathematics Competitions