Problem:
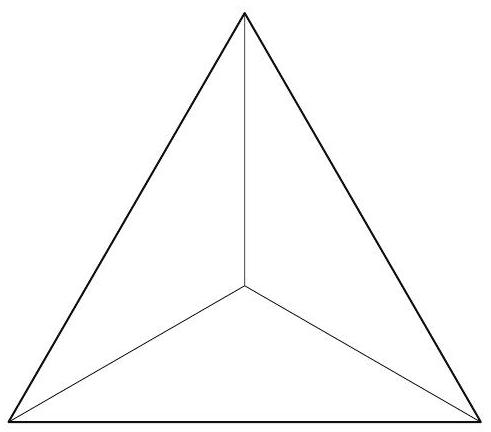
Three congruent isosceles triangles are constructed with their bases on the sides of an equilateral triangle of side length 1 . The sum of the areas of the three isosceles triangles is the same as the area of the equilateral triangle. What is the length of one of the two congruent sides of one of the isosceles triangles?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Let represent the altitude of each of the isosceles triangles from the base on the equilateral triangle. Then the area of each of the congruent isosceles triangles is . The sum of the areas of the three isosceles triangles is the same as the area of the equilateral triangle, so and . As a consequence, the Pythagorean Theorem implies that the side length of the isosceles triangles is
OR
Suppose that the isosceles triangles are constructed internally with respect to the equilateral triangle. Because the sum of their areas is equal to the area of the equilateral triangle, it follows that the center of the equilateral triangle is a vertex common to all three isosceles triangles. The distance from the center of the equilateral triangle to any of its vertices is two thirds of its height. Thus the required side length is equal to .
The problems on this page are the property of the MAA's American Mathematics Competitions