Problem:
Cyrus the frog sits on a flat surface. He jumps, landing feet away. He then chooses a direction at random and again jumps feet. What is the probability that after the second jump Cyrus lands within foot of his starting position?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Let be the starting position, and let be Cyrus's position after the first jump. Let and be the points at which the circle of radius 2 centered at (which consists of all of Cyrus's possible positions after the second jump) intersects the circle of radius 1 centered at .
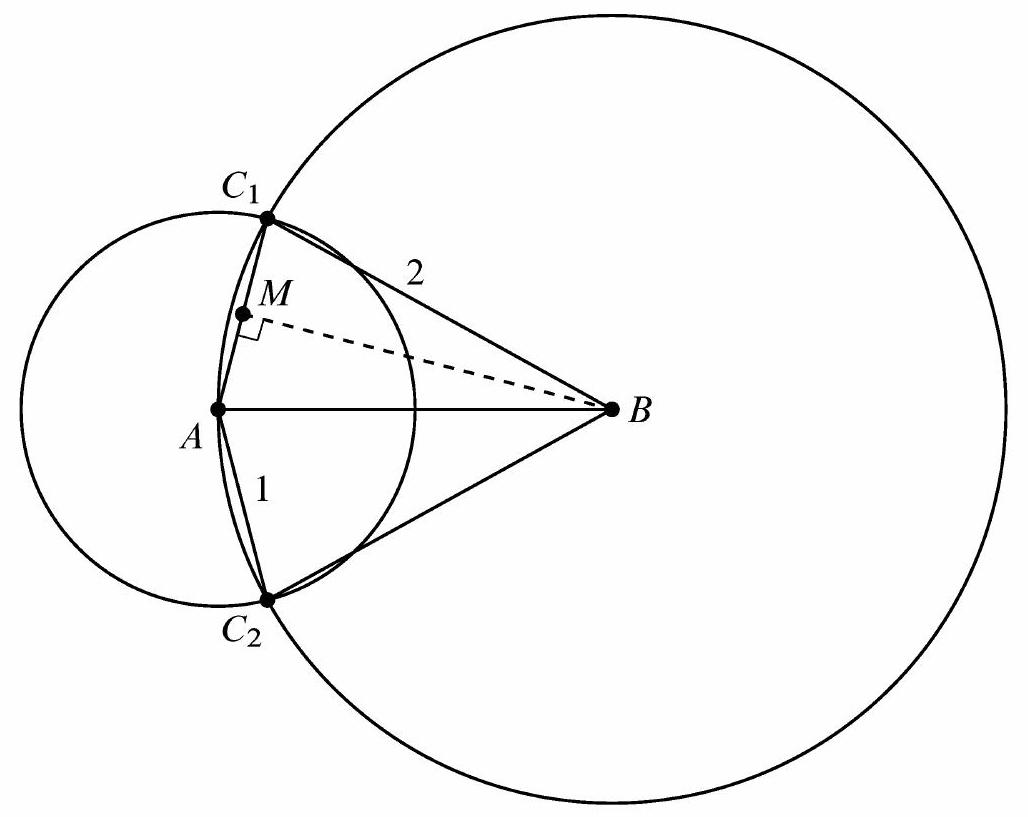
Cyrus will land within 1 foot of his starting position after the second jump if and only if he lands on minor arc . Therefore the requested probability is the fraction of the perimeter of the circle occupied by this arc. Let be the midpoint of . Because is isosceles, is a right angle.
Then
Note that . The fraction of the perimeter occupied by minor arc and the requested probability is therefore
This value is about 0.161 , slightly less than .
The problems on this page are the property of the MAA's American Mathematics Competitions