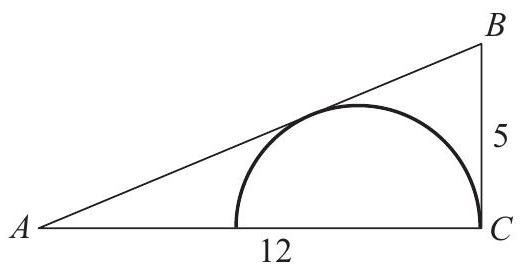
Problem:
In the right triangle ABC,AC=12,BC=5, and angle C is a right angle. A semicircle is inscribed in the triangle as shown. What is the radius of the semicircle?
Answer Choices:
A. 67
B. 513
C. 1859
D. 310
E. 1360
Solution:
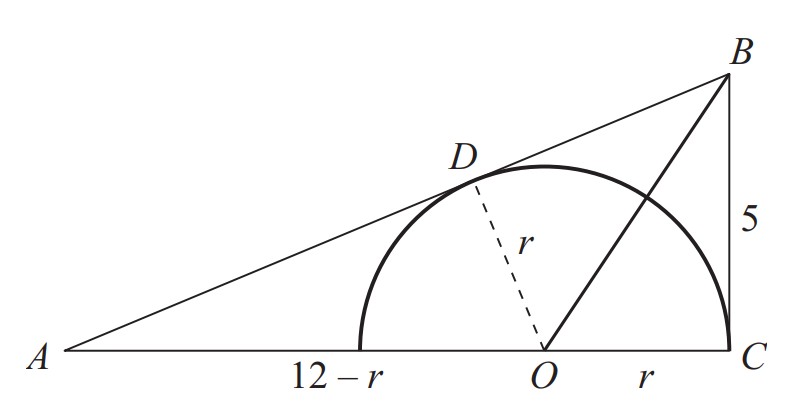
Let O be the center of the inscribed semicircle on AC, and let D be the point at which AB is tangent to the semicircle. Because OD is a radius of the semicircle it is perpendicular to AB, making OD an altitude of △AOB. By the Pythagorean Theorem, AB=13. In the diagram, OB partitions △ABC so that
Area(△ABC)=Area(△BOC)+Area(△AOB)
Since we know △ABC has area 30, we have
30=Area(△BOC)+Area(△AOB)=21(BC)r+21(AB)r=25r+213r=9r.
Therefore r=930=310.
OR
Because OD is a radius of the semicircle, it is perpendicular to AB, making △ADO similar to △ACB. Because BC and BD are both tangent to the semicircle, they are congruent. So BD=5 and AD=8. It follows that 8r=125 and so r=1240=310.
Answer: D.
The problems on this page are the property of the MAA's American Mathematics Competitions