Problem:
In square ABCE,AF=2FE and CD=2DE. What is the ratio of the area of â–³BFD to the area of square ABCE?
Answer Choices:
A. 61​
B. 92​
C. 185​
D. 31​
E. 207​
Solution:
Because the answer is a ratio, it does not depend on the side length of the square. Let AF=2 and FE=1. That means square ABCE has side length 3 and area 32=9 square units. The area of △BAF is equal to the area of △BCD=21​⋅3⋅2=3 square units. Triangle DEF is an isosceles right triangle with leg lengths DE=FE=1. The area of △DEF is 21​⋅1⋅1=21​ square units. The area of △BFD is equal to the area of the square minus the areas of the three right triangles: 9−(3+3+21​)=25​. So the ratio of the area of △BFD to the area of square ABCE is 925​​=185​.
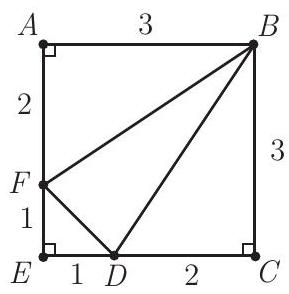
Answer: C​.
The problems on this page are the property of the MAA's American Mathematics Competitions
