Problem:
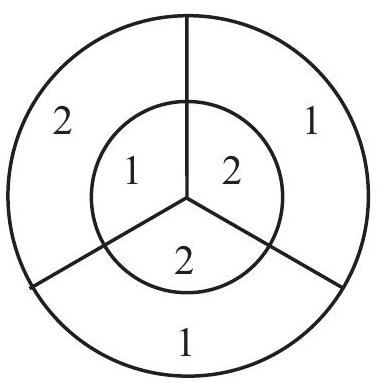
On the dart board shown in the figure, the outer circle has radius and the inner circle has radius . Three radii divide each circle into three congruent regions, with point values shown. The probability that a dart will hit a given region is proportional to the area of the region. When two darts hit this board, the score is the sum of the point values in the regions. What is the probability that the score is odd?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The outer circle has area and the inner circle has area , making the area of the outer ring . So each region in the outer ring has area , and each region in the inner circle has area . The probability of hitting a given region in the inner circle is , and the probability of hitting a given region in the outer ring is . For the score to be odd, one of the numbers must be and the other number must be . The probability of hitting a is
and the probability of hitting a is
Therefore, the probability of hitting a and a in either order is
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions