Problem:
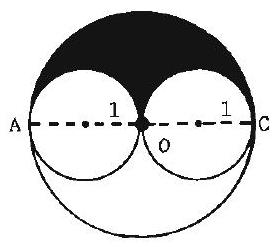
The large circle has diameter . The two small circles have their centers on and just touch at , the center of the large circle. If each small circle has radius , what is the value of the ratio of the area of the shaded region to the area of one of the small circles?
Answer Choices:
A. between and
B.
C. between and
D. between and
E. cannot be determined from the information given
Solution:
The radius of the large circle is since it is a diameter of a small circle. The area of the large circle is and the area of each small circle is . The shaded area is (by symmetry) half the difference of the areas of the large circle and the two small. circles, i.e. . Thus the desired ratio is .
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions