Problem:
A cricket randomly hops between leaves, on each turn hopping to one of the other leaves with equal probability. After hops, what is the probability that the cricket has returned to the leaf where it started?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
We begin by defining the action of the cricket jumping to the starting leaf as and the action of it jumping to any of the other three leaves as . With this in mind, note that when the cricket is on the first leaf, the probability of it jumping to the first leaf, , is zero, and the probability that it jumps to any of the other leaves, , is . Similarly, notice that when the cricket is not on the first leaf, and .
Therefore, let us map out all possible paths the cricket can take in four hops, and track the probability of each path as follows:
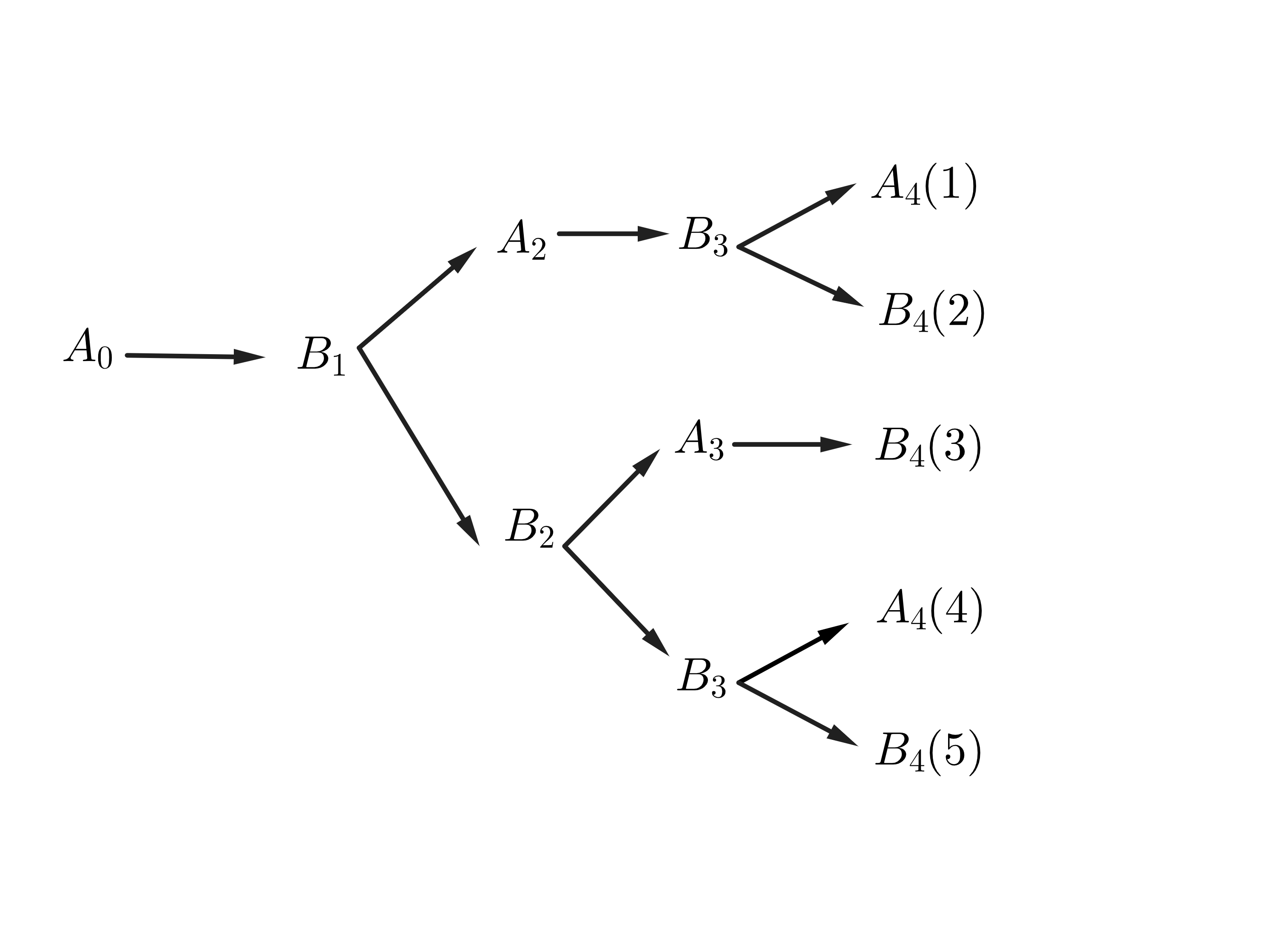
We want to find the total probability of the cricket landing on the first leaf, and as such, we want to find the total probability that the last node in the diagram is . This means that we want to find
Calculating this gives:
Thus, the answer is .
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions