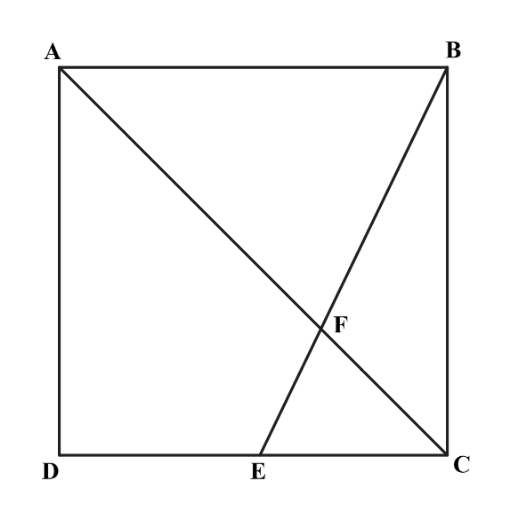
Problem:
Point E is the midpoint of side CD in square ABCD, and BE meets diagonal AC at F. The area of quadrilateral AFED is 45. What is the area of ABCD?
Answer Choices:
A. 100
B. 108
C. 120
D. 135
E. 144
Solution:
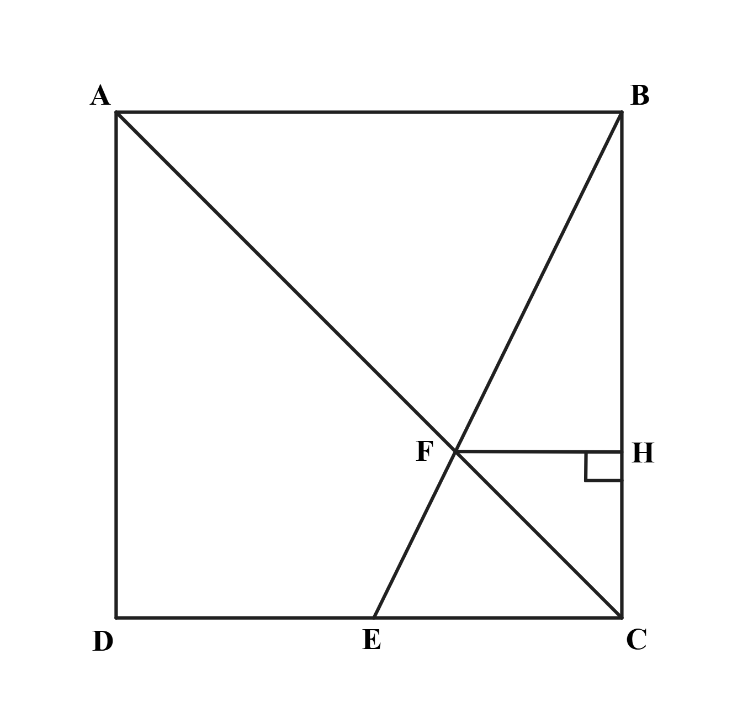
Let H be the point on BC where the altitude from F to BC meets BC. This altitude, FH, is illustrated above. Then, by angle-angle similarity, we can see that △CAB∼△CFH and △BFH∼△BEC. Since the sides of similar triangles are proportional, we know that BHFH=BCEC and HCFH=BCAB. Thus, ECFH=BCBH and ABFH=BCHC.
Adding these equations yields
ECFH+ABFH=BCBH+BCHC=BCBH+HC=BCBC=1.
This, in turn, goes to show that EC1+AB1=FH1.
Now, let s be the side length of the square. We know AB=2⋅EC=s. This means FH1=EC1+AB1=a1+a2=a3. Therefore, FH=3s.
Now, to compute the area of △EFC, we take the area of △BCE and subtract the area of △BFC. This is equal to
BC⋅EC2−BC⋅FH2=BC⋅(EC−FH)2=s⋅(2s−3s)2=s⋅(6s)2=12s2.
The area of AFED is the area of △ACD minus the area of △EFC, which is equal to
2s2−12s2=125s2=45.
With 125s2=45, we get s2=108, which is the area of the full square.
Answer: B.
The problems on this page are the property of the MAA's American Mathematics Competitions