Problem:
A square with an integer side length is cut into squares, all of which have integer side length and at least of which have area . What is the smallest possible value of the length of the side of the original square?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The area of the original square is a square number that is more than , so is the least possible value for the area of the original square. Its side has length . Two possible ways of cutting the square are shown below:
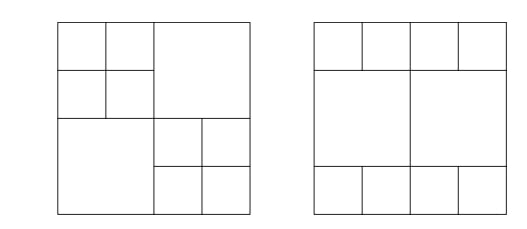
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions