Problem:
In a sign pyramid a cell gets a if the two cells below it have the same sign, and it gets a if the two cells below it have different signs. The diagram below illustrates a sign pyramid with four levels. How many possible ways are there to fill the four cells in the bottom row to produce a at the top of the pyramid?
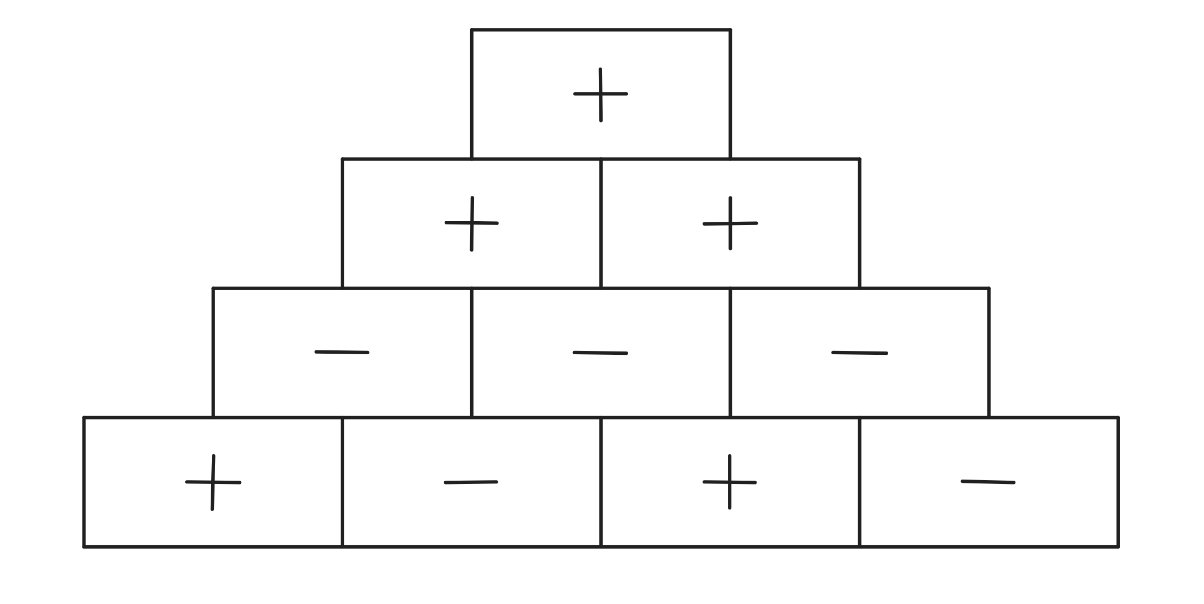
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Suppose we have two cells and the cell above them. If we are given the bottom left cell and the top cell, we can always find the bottom right cell as follows: - If the top cell is , then the bottom right cell must be the same as the bottom left cell. - If the top cell is , then the bottom right cell must be the opposite of the bottom left cell. Now, suppose we are given a row. Then, suppose we choose a value for the cell below and to the left of the leftmost cell in our given row. We then can inductively determine the entire row below our given by first finding the bottom-right cell of the leftmost cell in our row, and using that newly found cell as the bottom-left reference for the second to the left cell in the given row to find its bottom-right counterpart. The process continues on until the row below the given row is fully solved. Therefore, since we know that the top row has a cell labelled , we have choices for the row below, depending on our choice of the bottom-left cell. Similarly, we have choices for the third row, and thus choices for the fourth row. This gives total choices for the bottom row of the sign pyramid. Thus, the correct answer is .
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions