Problem:
Minh enters the numbers through into the cells of a grid in some order. She calculates the product of the numbers in each row and column. What is the least number of rows and columns that could have a product divisible by
Answer Choices:
A.
B.
C.
D.
E.
Solution:
We first need to note that there are multiples of from through . If any row or column has a multiple of , then the product of the numbers in the row or column will be divisible by . From this, it is evident that we must try to place all multiples of together in some corner of the grid so the least number of products will be divisible by . We can place multiples of in a grid so only rows and columns will have products that are divisible by . The remaining multiples of can then be placed in the column along the and row of the grid so in total we will only have columns and rows that have products divisible by , for a total of products divisible by . The diagram below illustrates our process. The highlighted cells contain the multiples of while the dotted lines mark the rows or columns that have products which are divisible by .
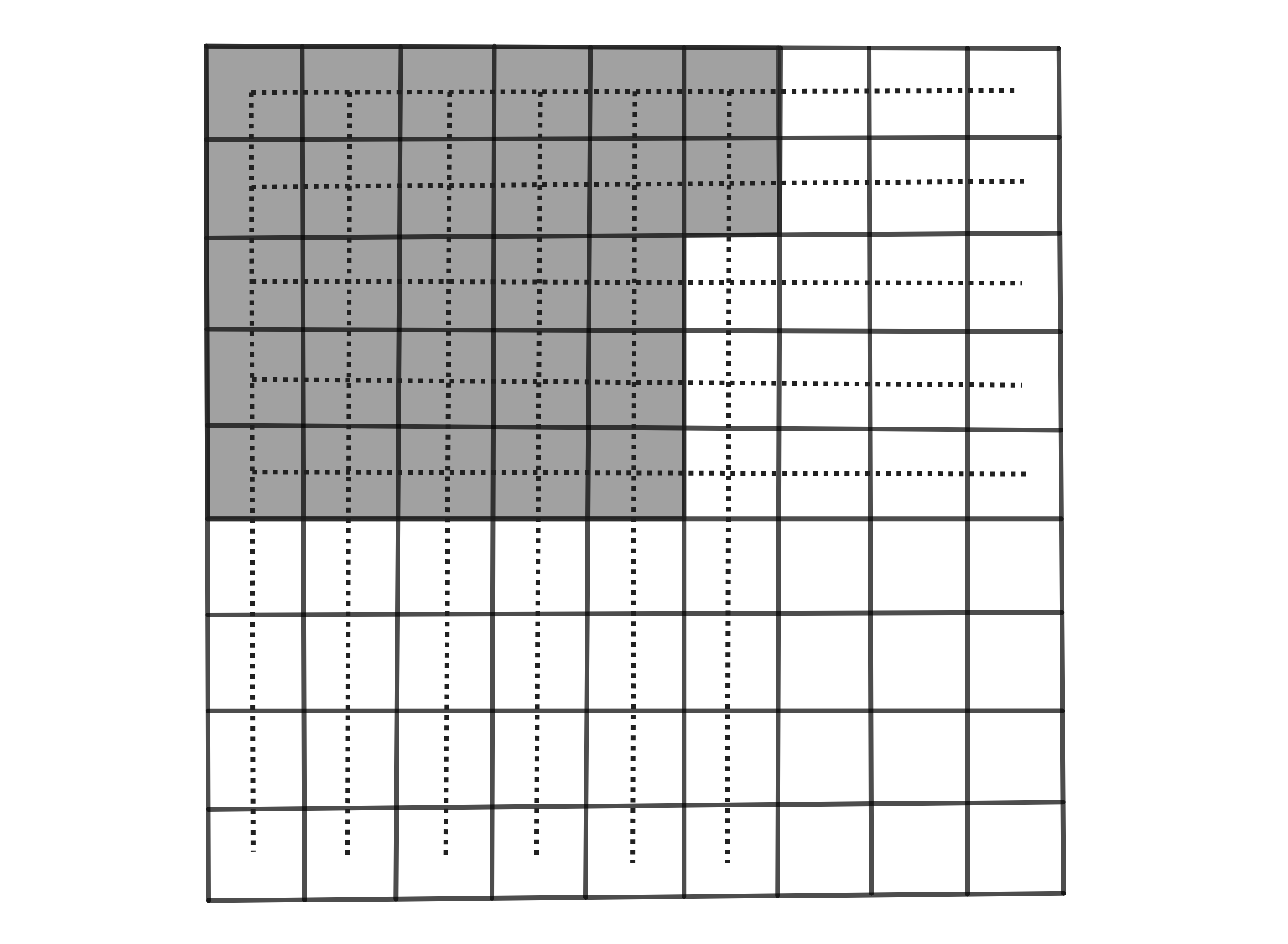
Thus, is the correct answer.
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions