Problem:
A "domino" is made up of two small squares:
Which of the "checkerboards" illustrated below CANNOT be covered exactly and completely by a whole number of non-overlapping dominoes?
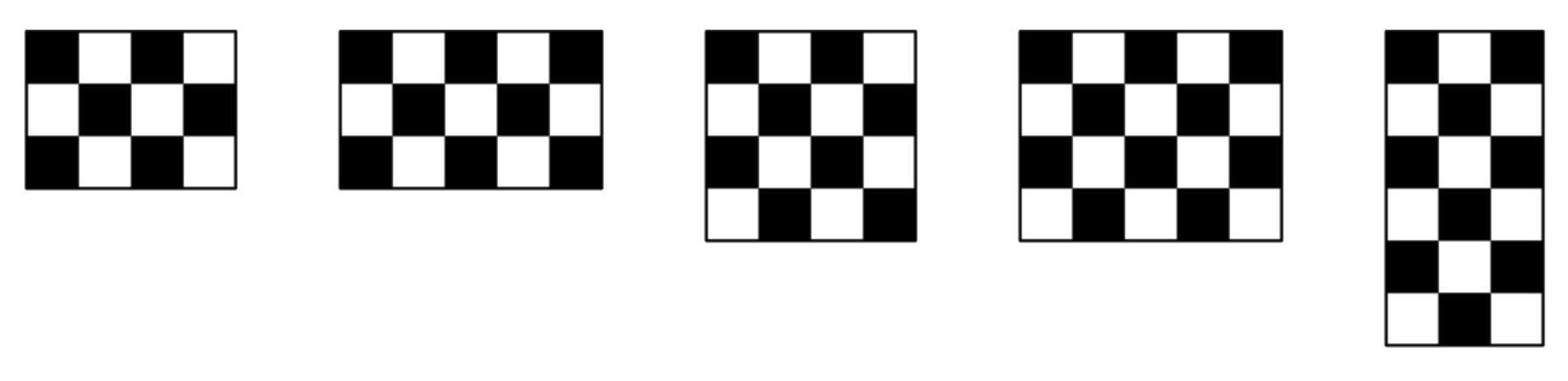
Answer Choices:
A.
B.
C.
D.
E.
Solution:
A collection of non-overlapping dominoes must cover an even number of squares. Since checkerboard has an odd number of squares, it follows that it cannot be covered as required. A little experimentation shows how the other checkerboards can be covered.
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions