Problem:
Pick two consecutive positive integers whose sum is less than . Square both of those integers and then find the difference of the squares. Which of the following could be the difference?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
One of the squares of two consecutive integers is odd and the other is even, so their difference must be odd. This eliminates and . The largest consecutive integers that have a sum less than are and , whose squares are and , with a difference of . Because the difference of the squares of consecutive positive integers increases as the integers increase, the difference cannot be . The difference between the squares of and is .
Let the consecutive integers be and , with . Then
That means the difference of the squares is an odd number. Therefore, the difference is an odd number less than or equal to , and choice is the only possible answer. The sum of and is .
Note: The difference of the squares of any two consecutive integers is not only odd but also the sum of the two consecutive integers. Every positive odd integer greater than and less than could be the answer.
Seen in geometric terms, looks like
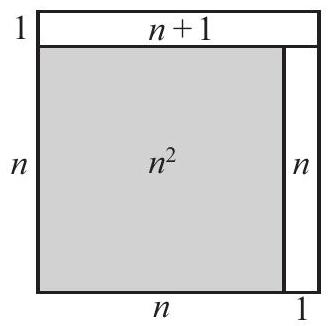
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions