Problem:
The midpoints of the four sides of a rectangle are:
What is the area of the rectangle?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Let the numbers be
This gives us the following rhombus:
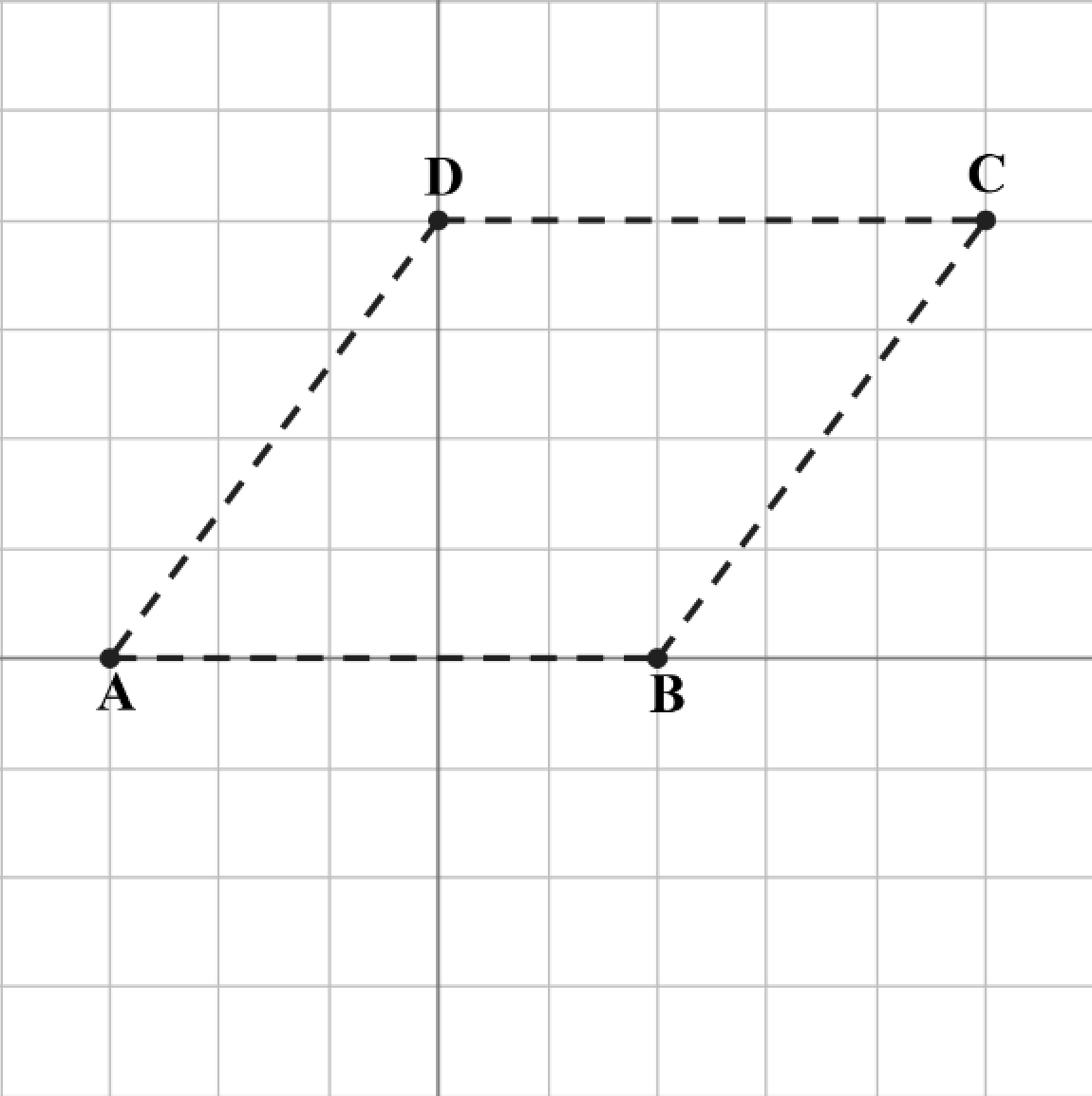
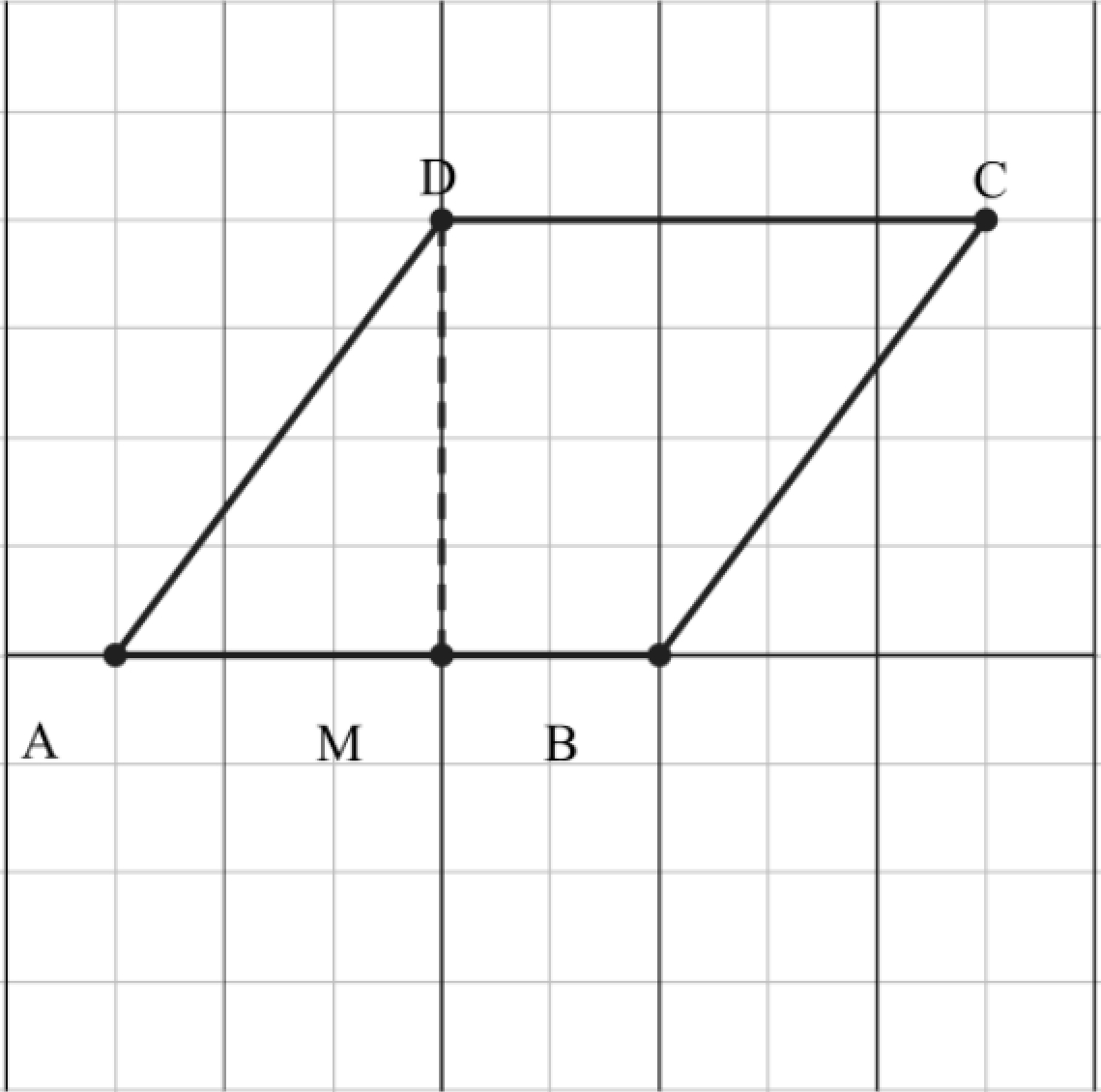
Now, moving away from the rhombus in question, let's consider more generally the relationship between a quadrilateral and the figure formed by its midpoints. Observe the arbitrary quadrilateral , its diagonals (dashed red), and the figure formed by its midpoints:
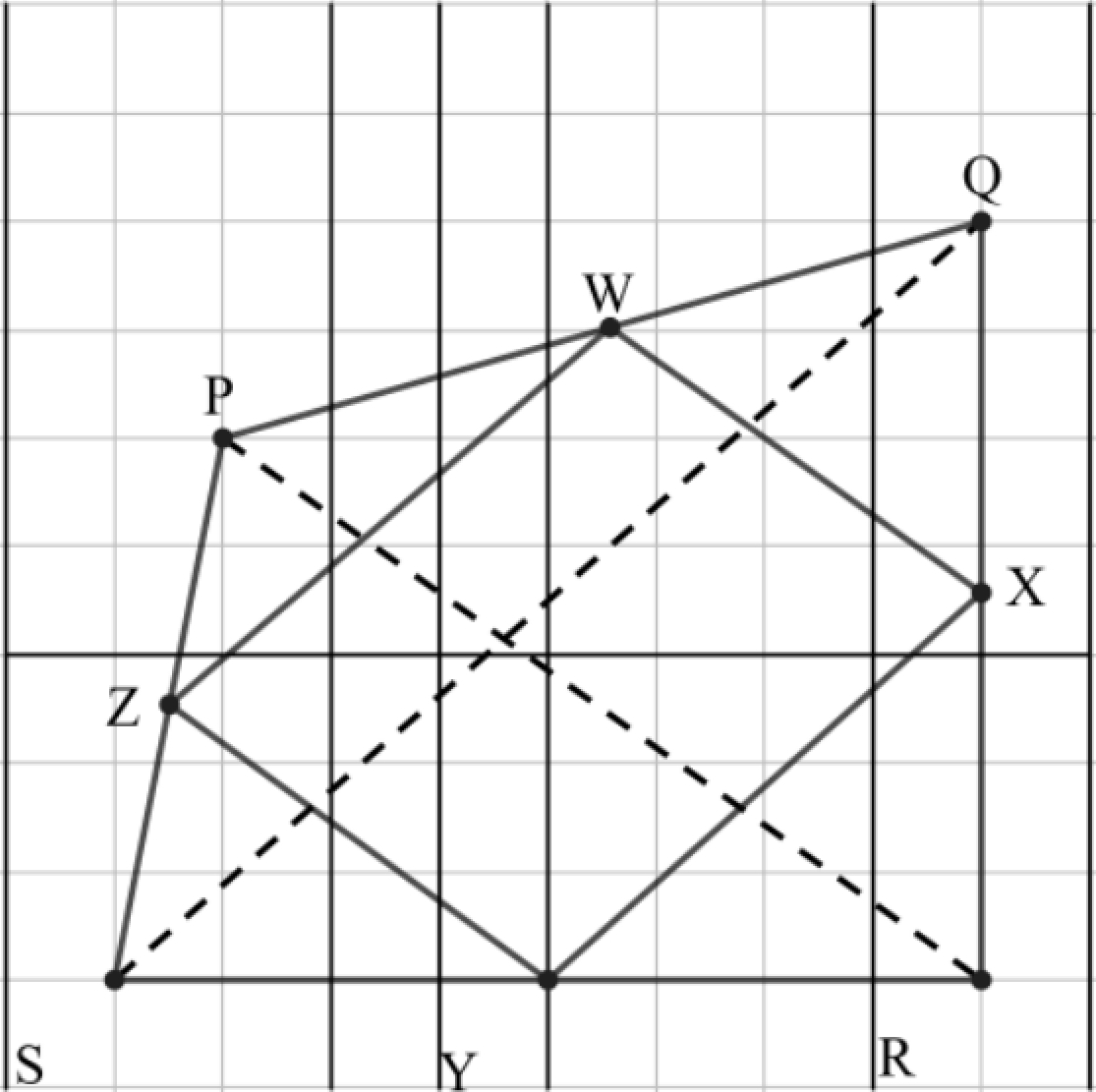
Note that the actual coordinates of don't matter, rather, as long as is a convex quadrilateral. Let's first consider the triangle . Notice that as is the midpoint of , and similarly, . Also notice that the angle is contained within both and . Therefore, we know that the two triangles are similar, and consequently, the side and the diagonal are parallel, and . We can use this same reasoning to show that the side and the diagonal are parallel, and . Furthermore, if we consider the triangles formed by the other diagonal , we can reapply this reasoning to show that the sides and the diagonal are parallel, and . Therefore, is a parallelogram where each of the unequal sides' lengths are equal to half the length of the corresponding parallel diagonal. With that in mind, notice that if we were to create a triangle out of , and the midpoint of , then the area of the right part of the parallelogram would be half the area of the new triangle formed, which would be . Similarly, it is clear that the area of the bottom left part of the parallelogram is half the area of . Adding those two parts up shows that the area of is half that of . With that in mind, let's go back to the original problem. Calculating the area of :
And as the area of is half that of the quadrilateral whose midpoints created it, we can conclude that the parent quadrilateral has an area of .
Thus, the answer is .
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions