Problem:
Squares , and are equal in area. Points and are the midpoints of sides and , respectively. What is the ratio of the area of the shaded pentagon to the sum of the areas of the three squares?
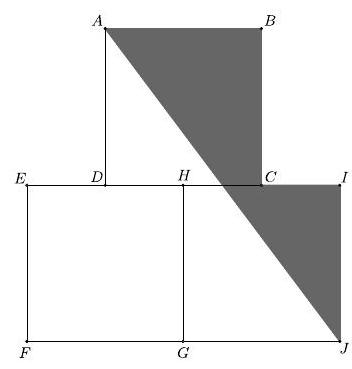
Answer Choices:
A.
B.
C.
D.
E.
Solution:
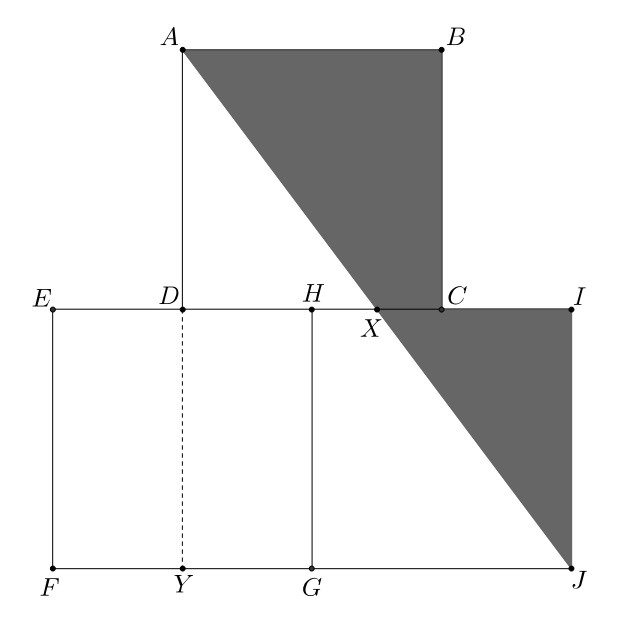
Let the length of the side of each square be and extend side to as shown. The total area of the three squares is . The unshaded area is area + area , so the shaded area is and the desired ratio is .
Label point as shown. Intuitively, rotating about takes it to so the shaded area is the same as the area of square and the desired ratio is . More precisely, segments , and are parallel to segments , and , respectively. Also, , so is congruent to .
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions