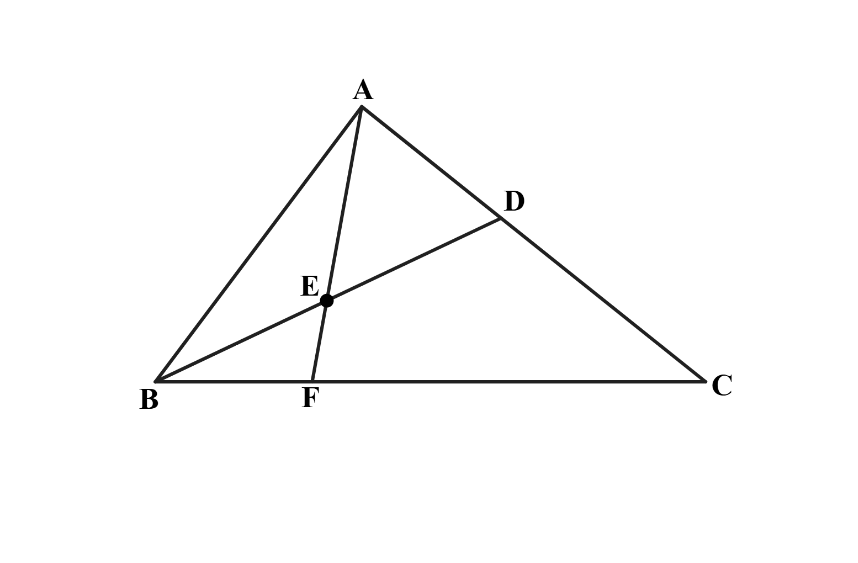
Problem:
In triangle , point divides side such that . Let be the midpoint of and let be the point of intersection of line and line . Given that the area of is , what is the area of triangle
Answer Choices:
A.
B.
C.
D.
E.
Solution:
We know that the area of is twice that of since its base is twice as long and they have the same heights. This tells us that the area of is . Similarly, we get that the area of is .
Note that . This tells us that the altitude of is the altitude of . We also know that , which tells us that the altitude of is the altitude of . Finally, we get that the altitude of is .
Note that the altitude of is the same as the altitude of . This tells us that the area of is the area of since they have the same base but different altitudes. This gives us the following equation, where equals the area of :
Cross-multiplying yields:
Thus, the correct answer is .
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions