Problem:
The one-way routes connecting towns and are shown in the figure below (not drawn to scale). The distances in kilometers along each route are marked. Traveling along these routes, what is the shortest distance from to in kilometers?
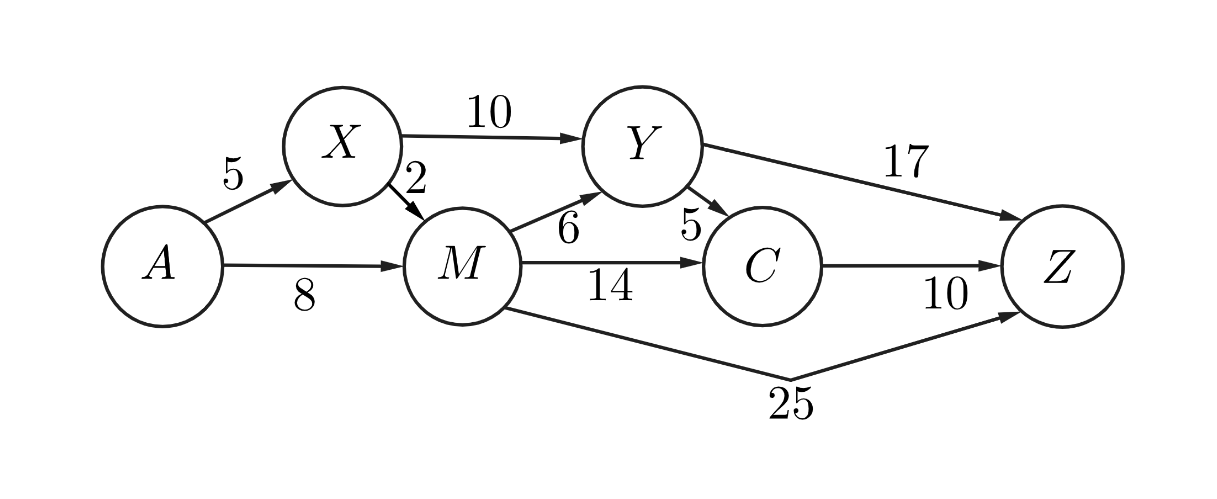
Answer Choices:
A.
B.
C.
D.
E.
Solution:
A systematic way of tracking the shortest overall distance to is to consider the shortest distance to get to each town from . For instance, the shortest distance to get to town from is km, trivially. Then, for town , going to town first will be shorter compared to going directly from , so the shortest path to town has a length of km. For town , it will take us km if we come from town and only km coming from , so km is the length of the shortest path to from . Doing the same for town will give us km as the shortest distance by coming from town . Finally, for town , we can either come from town , , or . The total distance if we come from each of these three towns respectively would be , , and . Hence, km is the shortest distance from to . The diagram below summarizes our process. Here, the town name is replaced by the shortest distance to get to that town from town .
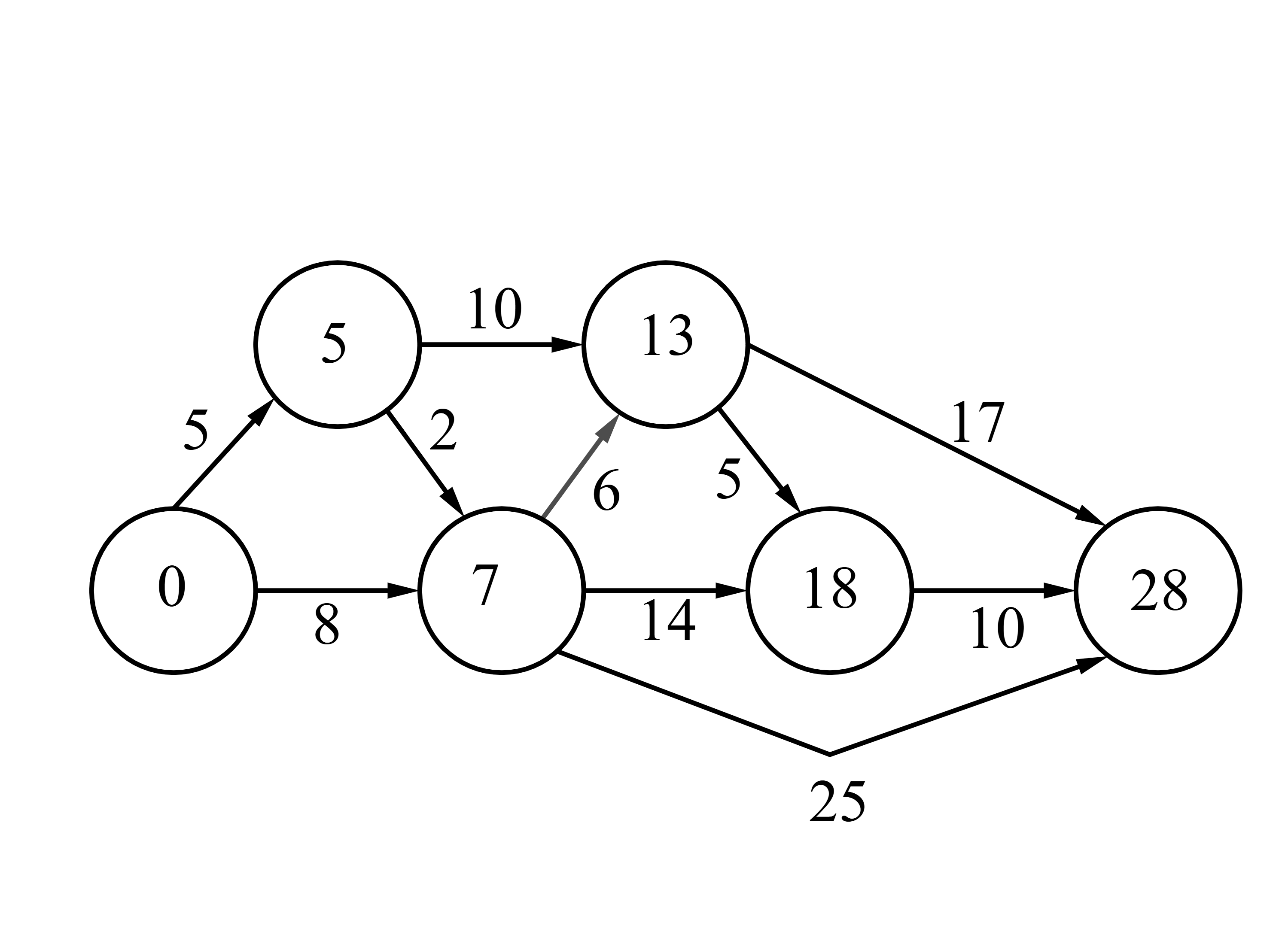
Thus, is the correct answer.
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions