Problem:
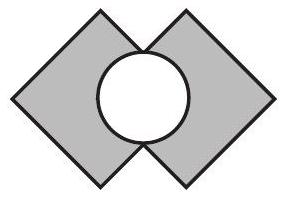
Two squares intersect at right angles, bisecting their intersecting sides, as shown. The circle's diameter is the segment between the two points of intersection. What is the area of the shaded region created by removing the circle from the squares?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The overlap of the two squares is a smaller square with side length , so the area of the region covered by the squares is . The diameter of the circle has length , the length of the diagonal of the smaller square. The shaded area created by removing the circle from the squares is .
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions