Problem:
A triangle with vertices at , and is plotted on a grid. What fraction of the grid is covered by the triangle?
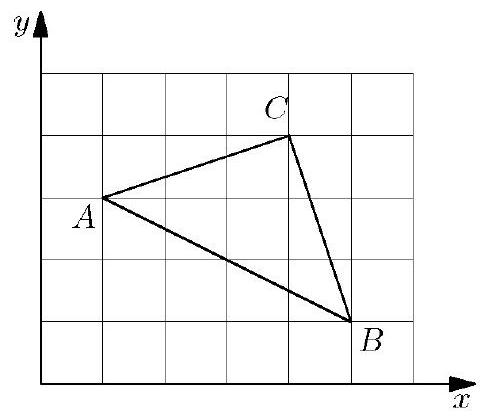
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The triangle is inscribed in a rectangle with vertices at , and . Three triangular regions are inside the rectangle but outside . The area of the lower-left triangle is square units. The area of the upper-left triangle is square units. The area of the third triangle is also square units. So the area of is square units. The area of the grid is square units. Thus, the fraction covered by the triangle is .
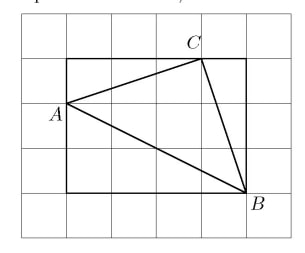
Pick's Theorem says that the area of a polygonal region whose vertices are at lattice points (points whose coordinates are integers) is given by where is the number of lattice points in the interior of the region and is the number of lattice points on the boundary. Referring to the figure above, there are lattice points on the boundary of at , and . There are points with integer coordinates in the interior of at , , and . Then the area of is square units. As before, the fraction of the rectangle covered by the triangle is .
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions