Problem:
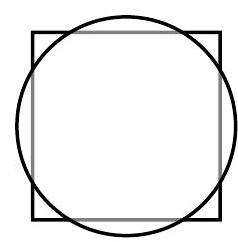
A square with side length and a circle share the same center. The total area of the regions that are inside the circle and outside the square is equal to the total area of the regions that are outside the circle and inside the square. What is the radius of the circle?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Because the circle and square share the same interior region and the area of the two exterior regions indicated are equal, the square and the circle must have equal area. The area of the square is or . Because the area of both the circle and the square is . Solving for , the radius of the circle, yields , so .
Note: It is not necessary that the circle and square have the same center.
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions