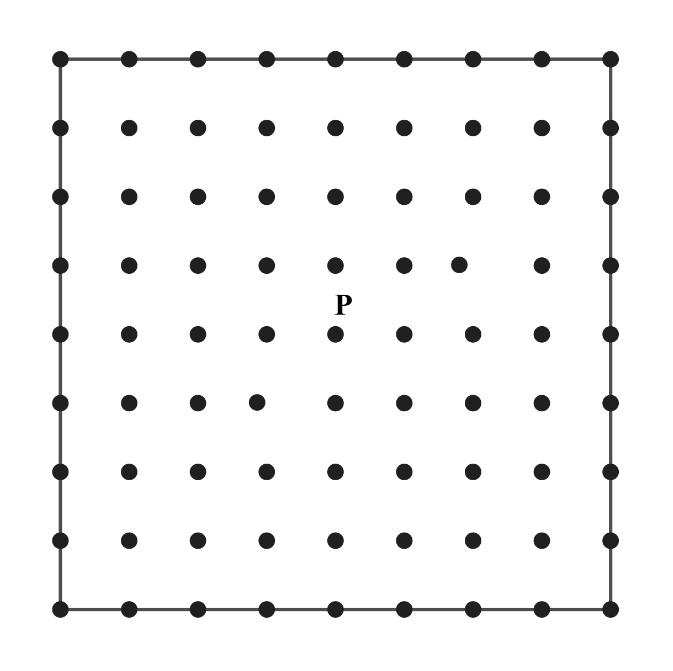
Problem:
There are grid points (uniformly spaced) in the square shown in the diagram below, including the points on the edges. Point is in the center of the square. Given that point is randomly chosen among the other points, what is the probability that the line is a line of symmetry for the square?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Note the only lines of symmetry for a square are the two diagonals and the two lines connecting opposite midpoints. Therefore, must be a point on any one of these four lines. Each line consists of points, for a total of points. Note that cannot be the same as , so we have to subtract out the points which coincide with , for a total of points. The probability is therefore .
Thus, the correct answer is .
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions