Problem:
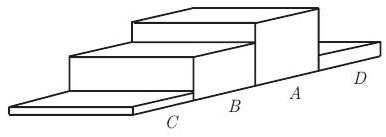
A one-cubic-foot cube is cut into four pieces by three cuts parallel to the top face of the cube. The first cut is foot from the top face. The second cut is foot below the first cut, and the third cut is foot below the second cut. From the top to the bottom the pieces are labeled and .
.jpg)
The pieces are then glued together end to end in the order , to make a long solid as shown below. What is the total surface area of this solid in square feet?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Looking from either end, the visible area totals square foot because piece measures , and the other pieces decrease in height from that piece. The two side views each show four blocks that can stack to a unit cube. So the area as seen from each side is . Finally, the top and bottom views each show four unit squares. So the top and bottom view each contribute to the area. Summing, the total surface area is
: Suppose the cuts are and . Does this change the solution?
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions