Problem:
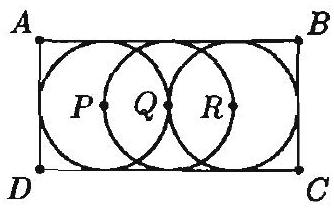
Three congruent circles with centers and are tangent to the sides of rectangle as shown. The circle centered at has diameter and passes through points and . The area of the rectangle is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Since the length of is the same as the diameter of the circle with center , it follows that . Since the circles with centers and are tangent to the parallel sides and , the diameters of these circles are also . The sum of the diameters of the circles with centers and gives the length of , so . Hence the area of the rectangle is .
The radius of the circle with center is , so . But and are also radii of the circles with centers and , respectively, so all three circles have radius . Hence and , so the area of the rectangle is .
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions