Problem:
Mr. Ramos gave a test to his class of students. The dot plot below shows the distribution of test scores.
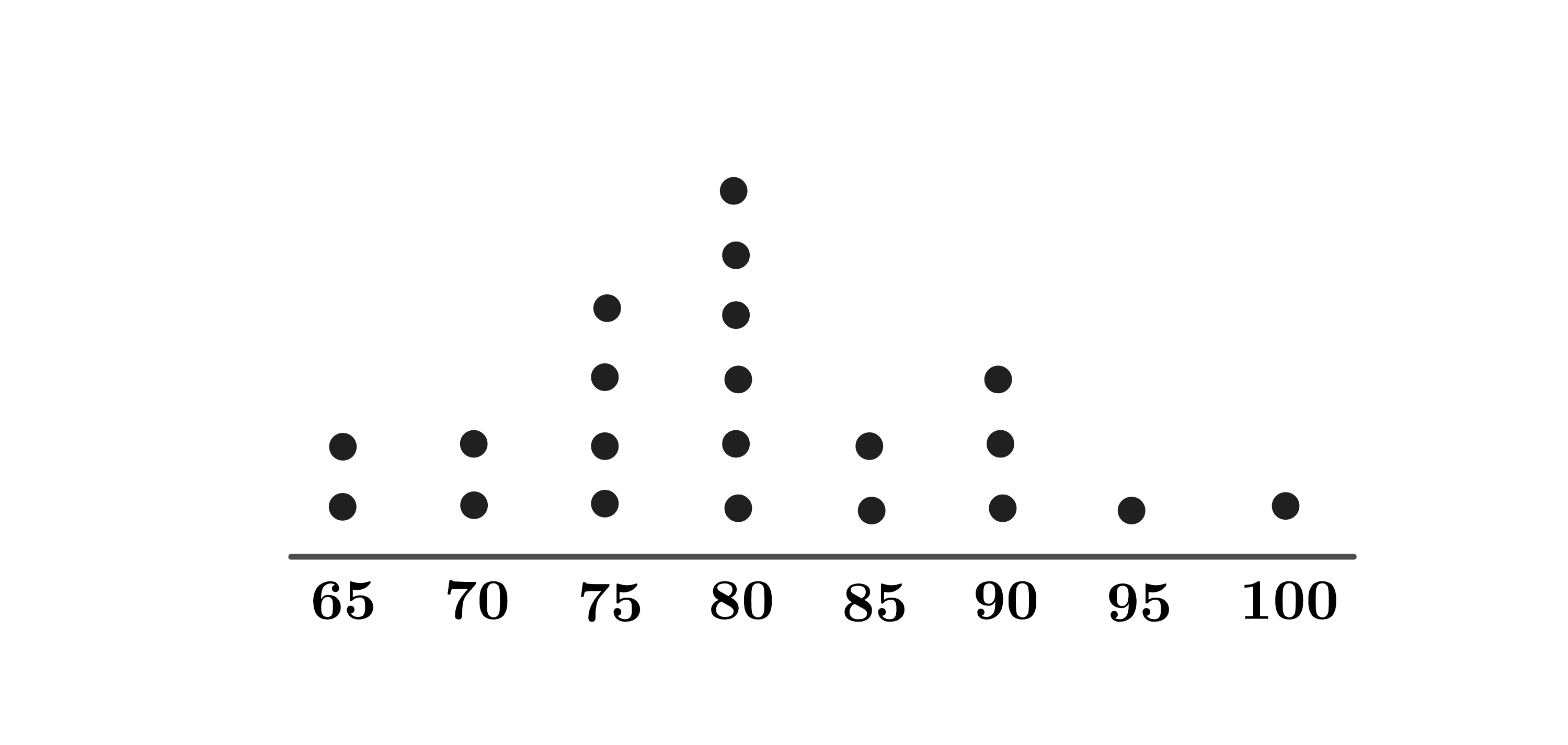
Later Mr. Ramos discovered that there was a scoring error on one of the questions. He regraded the tests, awarding some of the students extra points, which increased the median test score to . What is the minimum number of students who received extra points? (Note that the median test score equals the average of the scores in the middle if the 20 test scores are arranged in increasing order.)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
To make the median equal to , the average between the th and th highest scores must be . Therefore, we either have the th best and th best scores being or having the th best score be above and the th best score be under . The second option involves not having any scores of . If we move all the scores out of , we have only scores greater than . We can't move any other score to be greater than . Therefore, this scenario can't happen. Therefore, we must have the th and th best scores be . There are currently scores greater than or equal to , so we must add more scores so the th best score is .
Thus, the answer is .
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions