Problem:
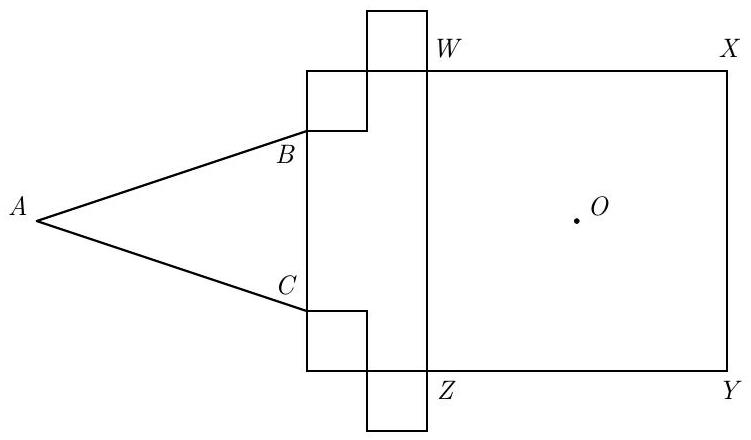
In the figure, the area of square WXYZ is 25 cm2. The four smaller squares have sides 1 cm long, either parallel to or coinciding with the sides of the large square. In △ABC, AB=AC, and when △ABC is folded over side BC, point A coincides with O, the center of square WXYZ. What is the area of △ABC, in square centimeters?
Answer Choices:
A. 415
B. 421
C. 427
D. 221
E. 227
Solution:
Let M be the midpoint of BC. Since △ABC is isosceles, AM is an altitude to base BC. Because A coincides with O when △ABC is folded along BC, it follows that AM=MO=25+1+1=29 cm. Also, BC= 5−1−1=3 cm, so the area of △ABC is 21⋅BC⋅AM=21⋅3⋅29=427 cm2.
Answer: C.
The problems on this page are the property of the MAA's American Mathematics Competitions
.jpg)