Problem:
A unit hexagram is composed of a regular hexagon of side length and its equilateral triangular extensions, as shown in the diagram. What is the ratio of the area of the extensions to the area of the original hexagon?
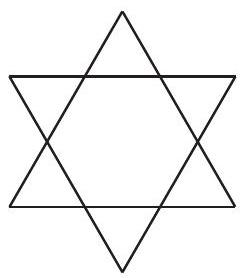
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Use diagonals to cut the hexagon into congruent triangles. Because each exterior triangle is also equilateral and shares an edge with an internal triangle, each exterior triangle is congruent to each interior triangle. Therefore, the ratio of the area of the extensions to the area of the hexagon is .
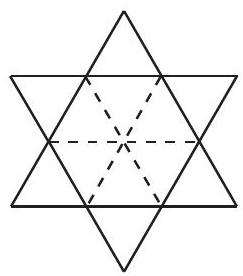
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions