Problem:
One-inch squares are cut from the corners of this 5 inch square. What is the area in square inches of the largest square that can be fitted into the remaining space?
Answer Choices:
A. 9
B. 1221
C. 15
D. 1521
E. 17
Solution:
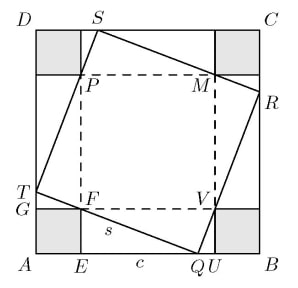
Let EQ=c and TQ=s as indicated in the figure. Triangles QUV and FEQ are similar since ∠FQE and ∠QVU are congruent because both are complementary to ∠VQU. So
UVQU=EQFE
and thus QU=c1. Then AB=1+c+1/c+1=5 and so c+1/c=3. Since the area of square ABCD equals the sum of areas of square QRST, four unit squares, four 1×c triangles, and four c1×1 triangles, it follows that
25===s2+4(1+2c+2c1)s2+4+2(c+c1)s2+4+2⋅3
Therefore, the area of square QRST=s2=15.
OR
Square FVMP has area 9, the four triangles FQV,VRM,MSP, and PTF each have area 23. So the area of square STQR is 9+6=15.
Answer: C.
The problems on this page are the property of the MAA's American Mathematics Competitions