Problem:
In the diagram below, the diameter of each of the two smaller circles is the radius of the larger circle. If the two smaller circles have a combined area of square unit, then what is the area of the shaded region, in square units?
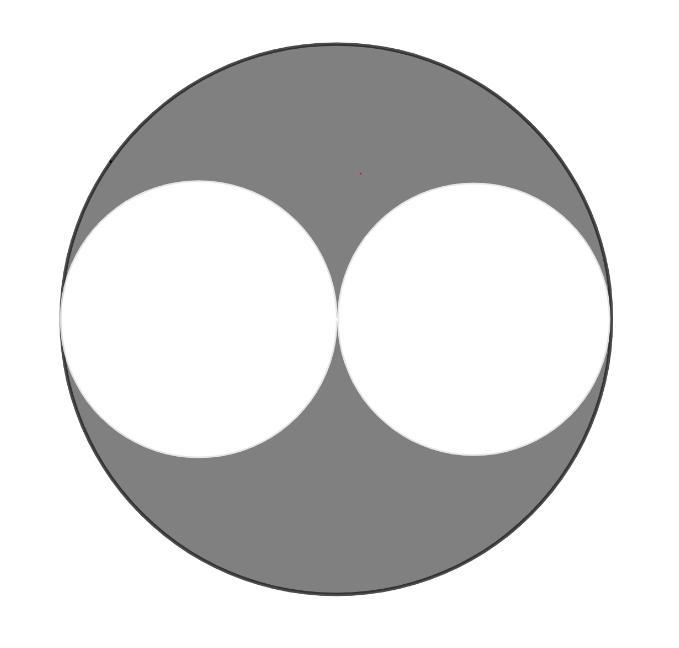
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Let be the area of the large circle. Since the diameter of each of the two smaller circles is itself the radius of the larger circle, the radius of the smaller circles is half that of the larger circle. Symbolically, if we allow to be the radius of the large circle and to be the radius of each of the smaller circles, .
As the area of the larger circle is equal to , the area of the smaller circles is:
Thus, the area of each smaller circle is , and the total area of the two smaller circles is:
As the area of two of these smaller circles combined is equal to square unit, we have:
As the area of the shaded region is equal to the area of the larger circle () minus the combined area of the two smaller circles , the area of the shaded region is:
Thus, the correct answer is .
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions