Problem:
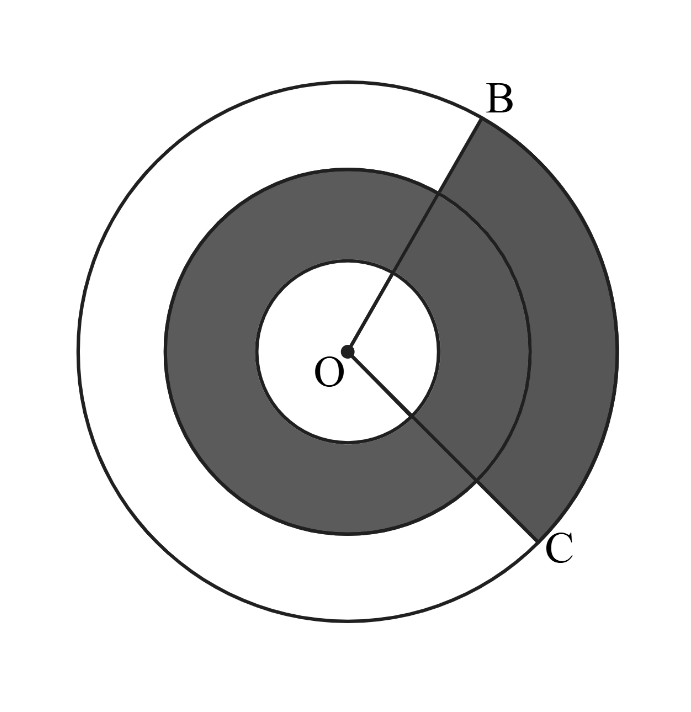
Three concentric circles centered at have radii of , and . Points and lie on the largest circle. The region between the two smaller circles is shaded, as is the portion of the region between the two larger circles bounded by the central angle , as shown in the figure below. Suppose the shaded and unshaded regions are equal in area. What is the measure of in degrees?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Let be the measure of . One component of the shaded region is the area of the circle with radius minus the area of the circle with radius . This part has area
The remaining area is a sector of the biggest circle minus the area of the circle with radius . This has area
Hence, the total area of the shaded region is
Next, we note that the unshaded region is composed of the smallest circle and the unshaded portion of the outer ring. This will have a total area of
Lastly, we equate the area of both regions and solve for :
This simplifies to
From here, we have
This further simplifies to
Solving for , we get
Thus, is the correct answer.
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions