Problem:
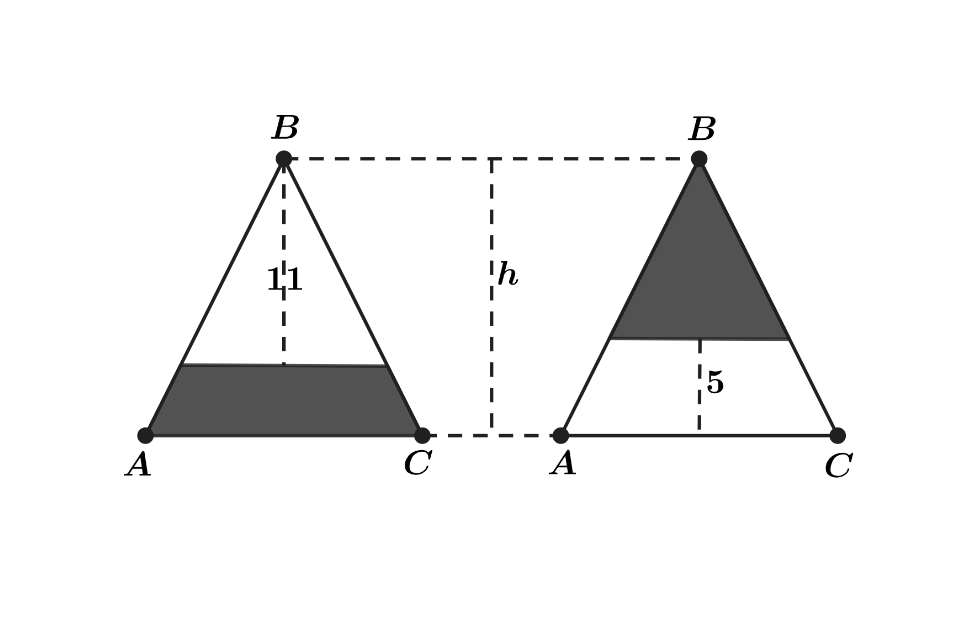
Isosceles triangle has equal side lengths and . In the figures below, segments are drawn parallel to so that the shaded portions of have the same area. The heights of the two unshaded portions are and units, respectively. What is the height of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Let be the area of . Note that the smaller triangles are similar to . This means that the ratio of their areas is the ratio of their side lengths squared. Then we get that
The left side is the area of the whole triangle minus the area of the unshaded region of the left triangle. The right-hand side is the area of the shaded triangle. We get this by finding the ratio of their side lengths (which is the same as the ratio of their heights) and squaring it. Simplifying yields . This simplifies to , so .
Thus, is the correct answer.
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions