Problem:
To promote her school's annual Kite Olympics, Genevieve makes a small kite and a large kite for a bulletin board display. The kites look like the one in the diagram. For her small kite Genevieve draws the kite on a one-inch grid. For the large kite she triples both the height and width of the entire grid.
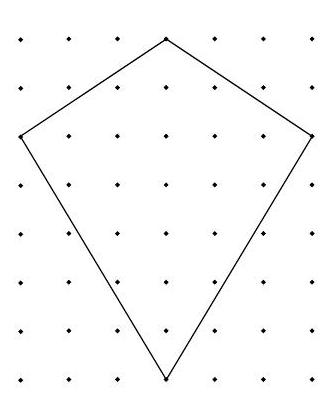
The large kite is covered with gold foil. The foil is cut from a rectangular piece that just covers the entire grid. How many square inches of waste material are cut off from the four corners?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The upper corners can be arranged to form a rectangle and the lower corners can be arranged to form a rectangle. The total area is square inches. (Note that the kite's area is also square inches.)
.jpg)
The area cut off equals the area of the kite. If each dimension is tripled, the area is times as large as the original area and square inches. In general, if one dimension is multiplied by a number and the other by a number , the area is multiplied by .
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions