Problem:
A semicircle is inscribed in an isosceles triangle with base and height so that the diameter of the semicircle is contained in the base of the triangle as shown. What is the radius of the semicircle?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Let be the midpoint of base of and the center of the semicircle. Triangle is a right triangle with and , and so, by the Pythagorean Theorem, . Let be the point where the semicircle intersects , so radius is perpendicular to . Then and are similar, and therefore, . Hence, and so .
Let be the center of the semicircle, which is also the midpoint of base . Since and , then by the Pythagorean Theorem . Let be the point where the semicircle intersects , so radius is perpendicular to . Since the area of is , then and so .
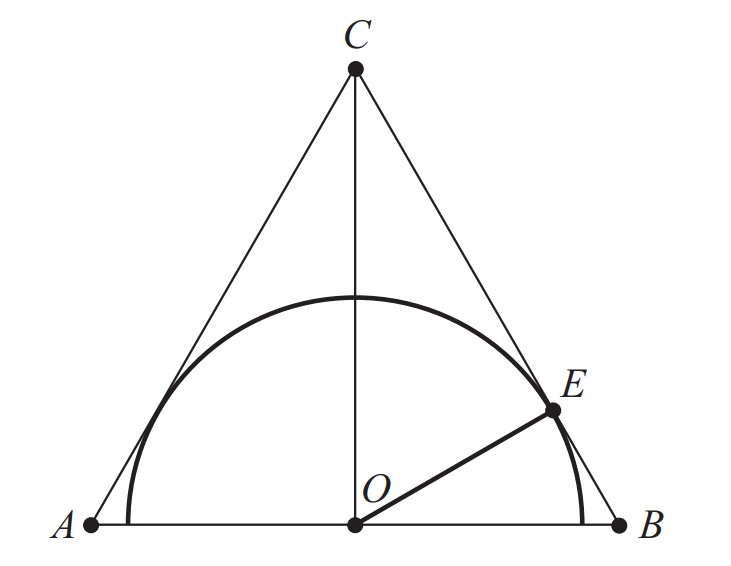
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions