Problem:
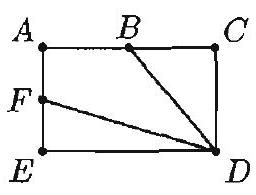
The rectangle shown has length AC=32, width AE=20, and B and F are midpoints of AC and AE, respectively. The area of the quadrilateral ABDF is
Answer Choices:
A. 320
B. 325
C. 330
D. 335
E. 340
Solution:
Rectangle ACDE has area 32×20=640. Triangle BCD has area (16×20)/2=160, and triangle DEF has area (10×32)/2=160. The remaining area, ABDF, is 640−(160+160)=320.
OR
Insert diagonal AD. The areas of triangles ABD and BCD are (AB)(CD)/2 and (BC)(CD)/2 which are equal since AB=BC. Hence half the area in the rectangle above AˉDˉ is in ABDF. Similarly, triangles ADF and DEF have equal areas, and half the area in the rectangle below AD is in ABDF. Thus, the area of ABDF is (32×20)/2=320.
OR
Draw a perpendicular from point B to ED to show that the area of △BCD is one fourth of the area of ACDE.
Similarly, draw a perpendicular from point F to CD to show that the area of △DEF is one fourth of the area of ACDE. Thus the area of ABDF is one half of the area of ACDE, or (32×20)/2=320.
Answer: A.
The problems on this page are the property of the MAA's American Mathematics Competitions
.jpg)
.jpg)