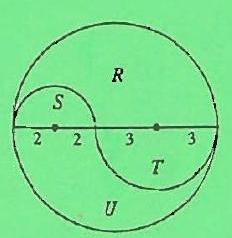
Problem:
ACE is divided at C in the ratio 2:3. The two semicircles, ABC and CDE, divide the circular region into an upper (shaded) region and a lower region. The ratio of the area of the upper region to that of the lower region is
Answer Choices:
A. 2:3
B. 1:1
C. 3:2
D. 9:4
E. 5:2
Solution:
Let the diameter of the large circle equal 10. Then the ratio is:
(Area of semicircle T+U)−(Area of semicircle T)+(Area of semicircle S)(Area of semicircle R+S)−(Area of semicircle S)+(Area of semicircle T)=21π52−21π32+2221π52−21π22+21π32=10π15π=23 or 3:2.
Answer: C.
The problems on this page are the property of the MAA's American Mathematics Competitions
.jpg)