Problem:
In the cube with opposite vertices and , and are the midpoints of segments and , respectively. Let be the ratio of the area of the cross-section to the area of one of the faces of the cube. What is
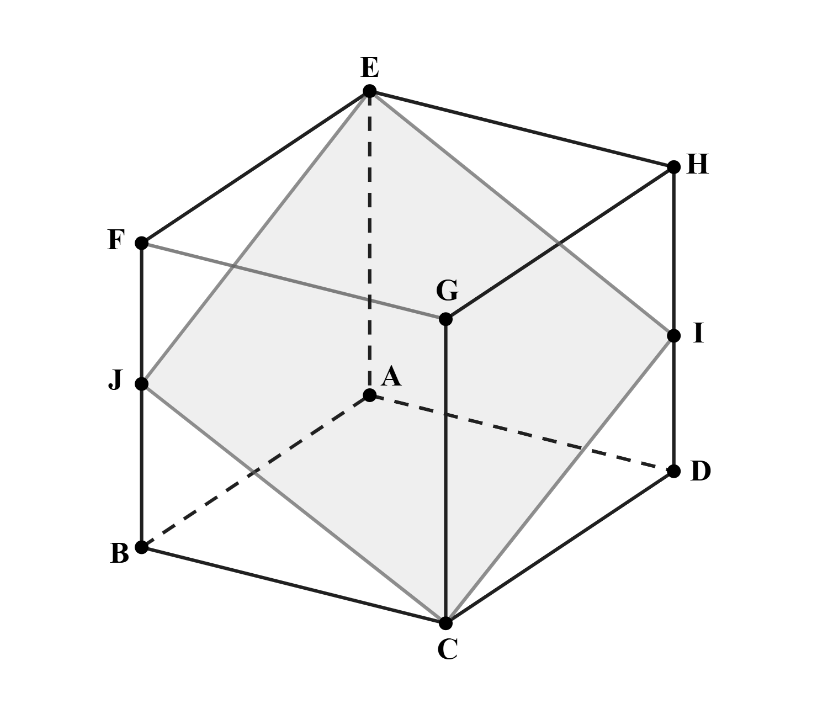
Solution:
Allow represent the length of an edge of the cube. Noting that each side of the cross-section is equal in length, we conclude that is a rhombus. The area of this rhombus can be calculated as:
since the area of a rhombus is equal to half the product of its diagonals. Using the Pythagorean Theorem, we find:
Similarly, using the Pythagorean Theorem again, we get:
Therefore, the area of the rhombus is:
Thus, , and the correct answer is .
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions