Problem:
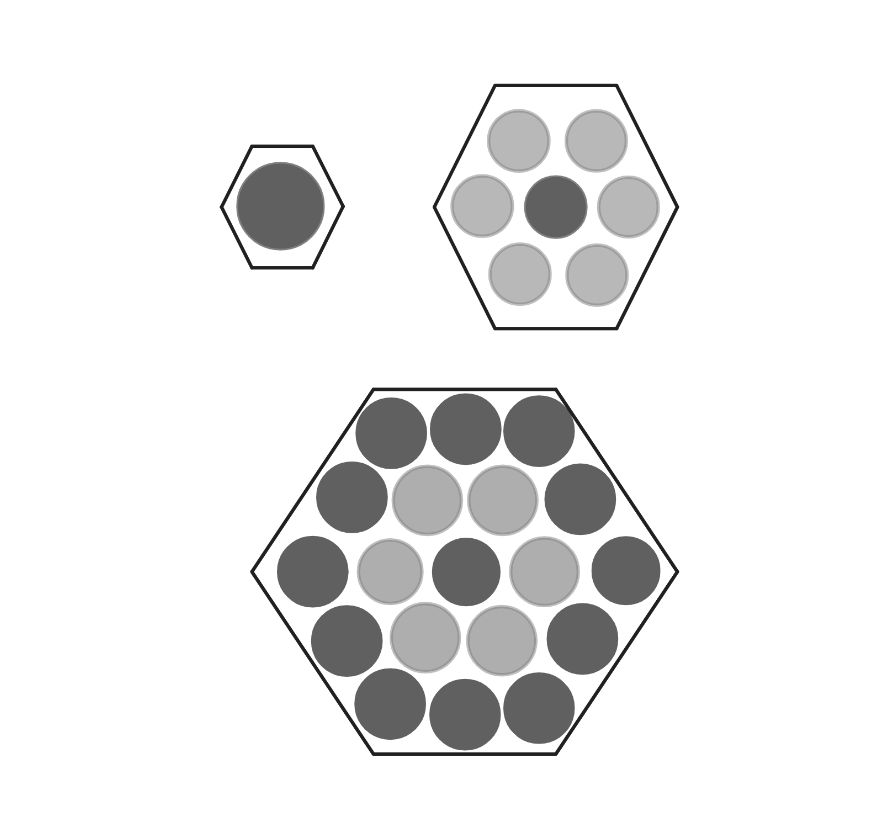
Three hexagons of increasing size are shown below. Suppose the dot pattern continues so that each successive hexagon contains one more band of dots. How many dots are in the next hexagon?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Firstly, let's try and find a pattern for the number of dots in the th ring. Notice that for the th ring, there are always dots on each edge of the hexagon. However, this overcounts, as each vertex of the hexagon is counted twice. Therefore, we can claim that for the th ring, the number of dots is equal to . Note that this pattern does not hold for .
Therefore, for the first hexagon, we have dot, the nd hexagon adds dots, the rd hexagon adds dots, as reflected in the diagram. Extending the pattern, we can say that the fourth hexagon adds dots.
Finally, notice that the total number of dots in the hexagon is equal to the sum of all the rings up to the th ring. This is the same as saying: . Therefore, for we have a total of
Thus, the correct answer is .
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions