Problem:
A point is chosen at random from within a circular region. What is the probability that the point is closer to the center of the region than it is to the boundary of the region?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Suppose that the circle has radius . Then, being closer to the center of the region than the boundary of the region (the circle) would mean the chosen point must be inside the circle of radius with the same center as the larger circle of radius . The area of the smaller region is , and the area of the total region is . Since the area of the smaller region is of the area of the total region, the required probability is .
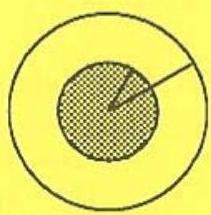
Note. The odds that the point is closer to the center are .
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions