Problem:
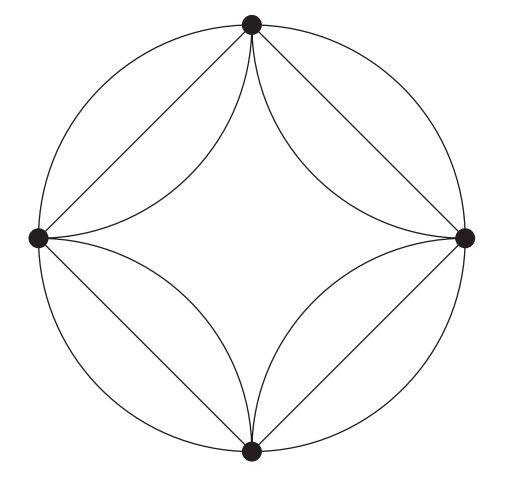
A circle of radius is cut into four congruent arcs. The four arcs are joined to form the star figure shown. What is the ratio of the area of the star figure to the area of the original circle?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Translate the star into the circle so that the points of the star coincide with the points on the circle. Construct four segments connecting the consecutive points of the circle and the star, creating a square concentric to the circle.
The area of the circle is . The square is made up of four congruent right triangles with area , so the area of the square is . The area inside the circle but outside the square is .
This is also the area inside the square but outside the star. So, the area of the star is . The ratio of the area of the star figure to the area of the original circle is .
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions