Problem:
Rectangle is inscribed in a semicircle with diameter , as shown in the figure. Let and . What is the area of
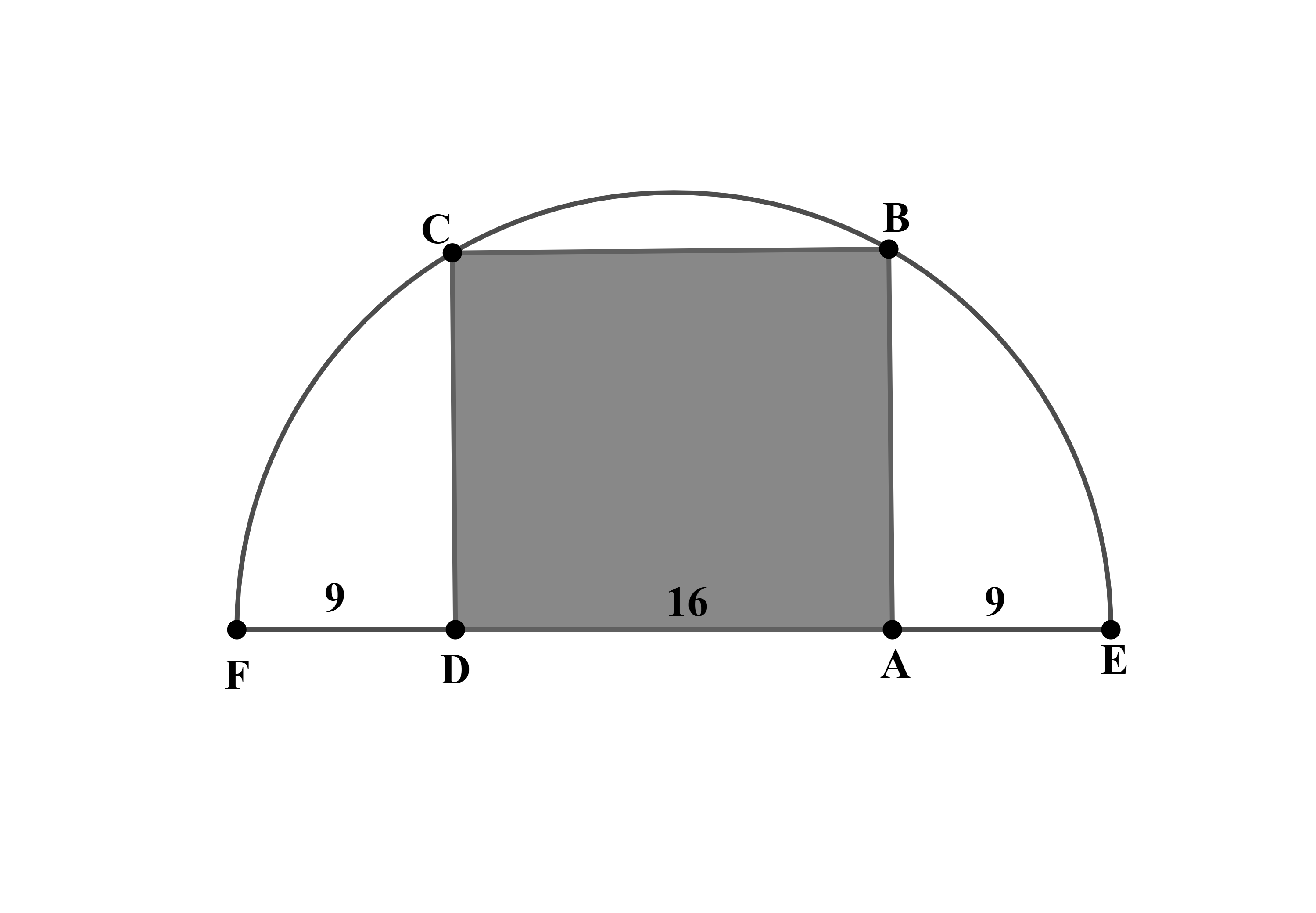
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Since is the diameter of the semicircle, we know the length of the diameter is , and so the radius is . Let be the center of the diameter. The length from to , denoted , is therefore . Since is on , we know . Substituting the known values:
Also, since we have a semicircle, we know . Finally, since is a rectangle, we know is a right angle. This means we can find using the Pythagorean Theorem. We know . Substituting the known values:
As such, the area of the rectangle is
Thus, the correct answer is .
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions