Problem:
Jean made a piece of stained glass art in the shape of two mountains, as shown in the figure below. One mountain peak is feet high and the other peak is feet high. Each peak forms a angle, and the straight sides of the mountains form angles with the ground. The artwork has an area of square feet. The sides of the mountains meet at an intersection point near the center of the artwork, feet above the ground. What is the value of
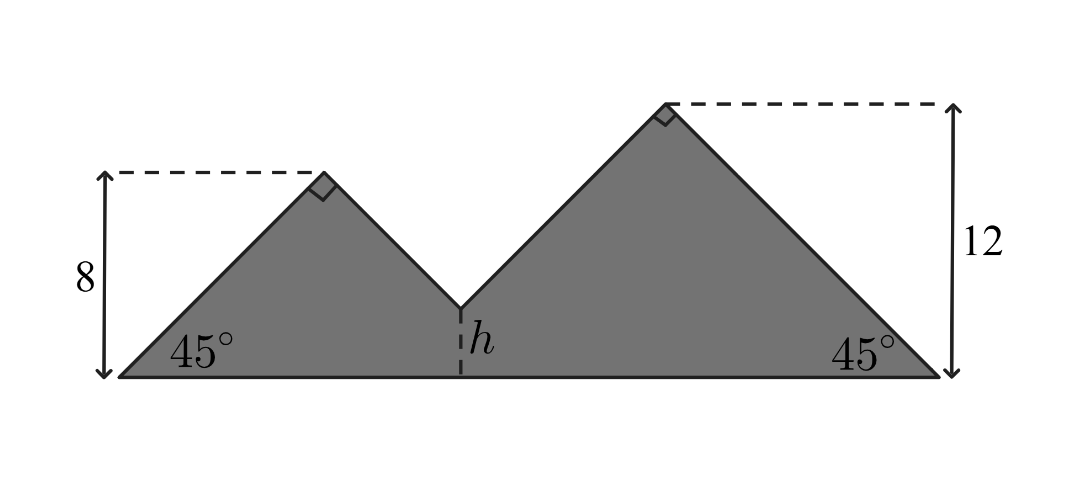
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Observe that we can extend the two mountains at the intersection point to make three triangles as shown in the diagram below.
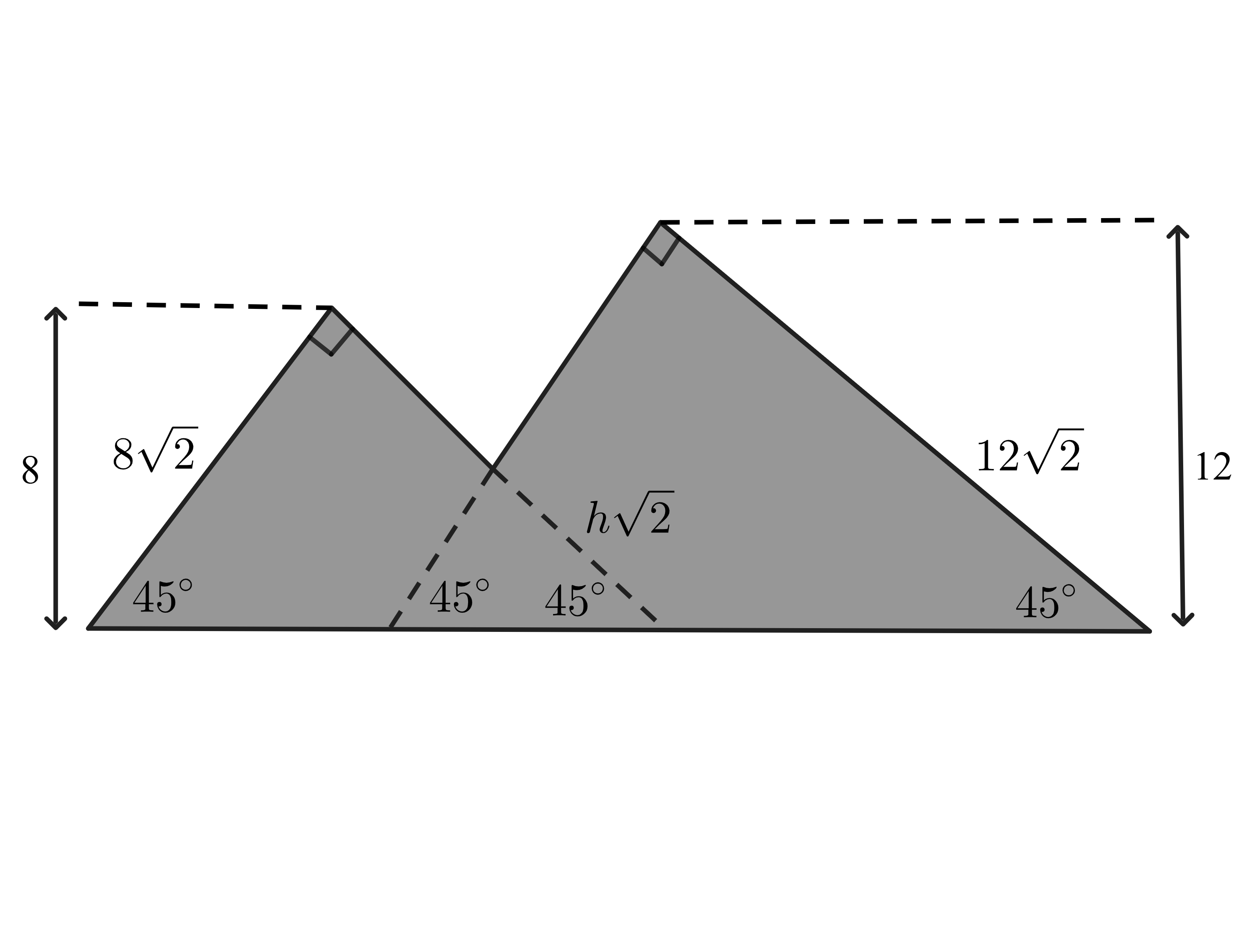
All triangles formed are triangles, and based on the given height information, we can determine that the side lengths of the triangles, from left to right, are , , and . Hence, we have areas of , , and , respectively. To find , we use the total area of the diagram, which we can obtain by adding the area of the two large triangles and subtracting the area of the triangle with height since this area was counted twice. Doing this, we get:
Rearranging this gives:
Thus,
Hence, is the correct answer.
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions