Problem:
A circle with radius is inscribed in a square and circumscribed about another square as shown. Which fraction is closest to the ratio of the circle's shaded area to the shaded area between the two squares?
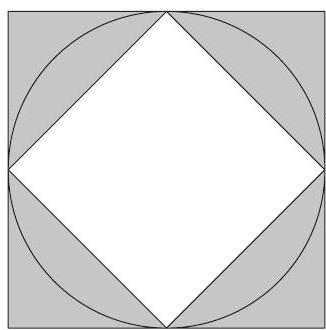
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The area of a circle of radius is . The side length of the big square is the diameter of the circle, which is , so its area is . The big square can be divided into congruent triangles, and the shaded area is made up of of those triangles. The shaded area is half the area of the big square, which is . The requested ratio of the two shaded areas is .
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions