Problem:
A rectangle is covered without overlap by three shapes of tiles: , , and , shown below. What is the minimum possible number of tiles used?
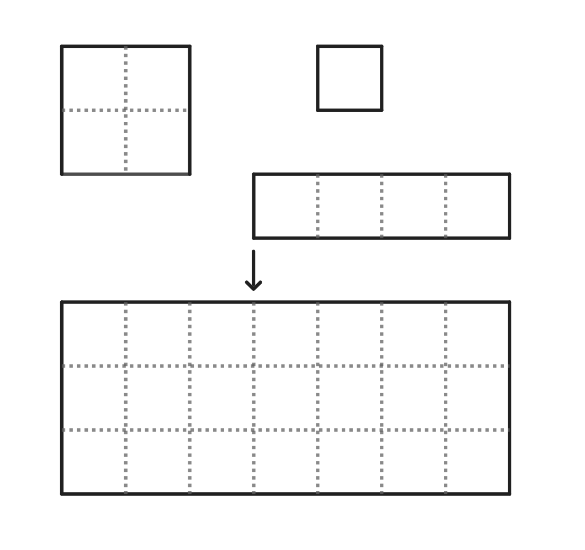
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Notice that if we only fill the rectangle using and tiles, then we will always be filling the rectangle in multiples of . From the answer choices, it will suffice to consider the cases where we are able to fill or tiles out of the tiles of the rectangle, since the former will leave us spaces for the tiles while the latter will leave us with one. The other options are not possible since those numbers of tiles cannot be arrived at by subtracting any multiple of from . By attempting to place the and tiles, we can immediately notice that it's not possible to fill tiles in the rectangle, and we can easily find cases where we are left with five tiles.
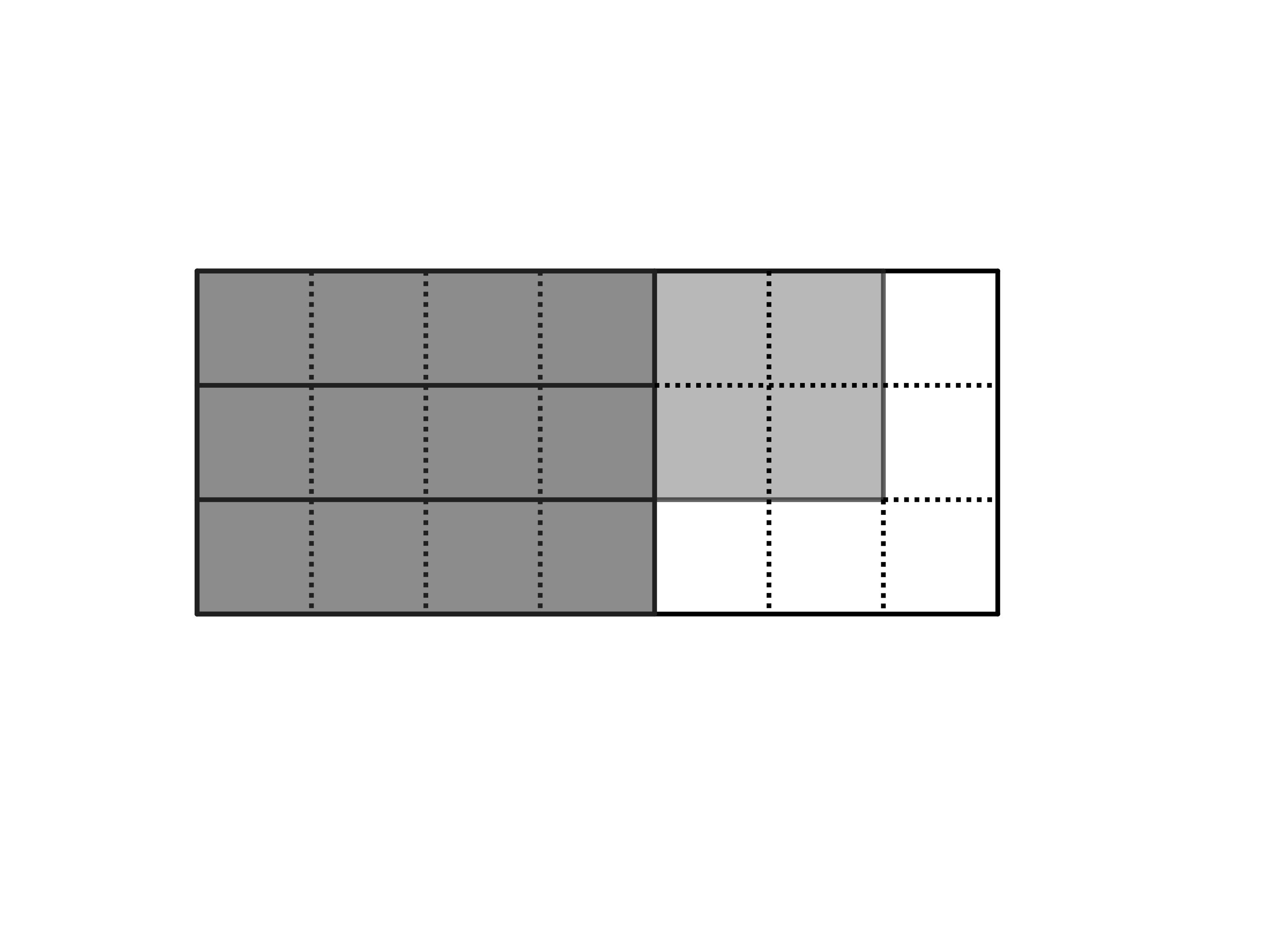
Thus, is the correct answer.
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions