Problem:
Samantha lives blocks west and block south of the southwest corner of City Park. Her school is blocks east and blocks north of the northeast corner of City Park. On school days she bikes on streets to the southwest corner of City Park, then takes a diagonal path through the park to the northeast corner of City Park, and then bikes on streets to school. If her route is as short as possible, how many different routes can she take?

Answer Choices:
A.
B.
C.
D.
E.
Solution:
There are ways she can bike from home to the southwest corner of the park, , , or . There are ways to bike from the northeast corner of the park to school, , , , , , or . So there are routes.
Using a Pascal's Triangle approach starting from the house to the school, count the routes to each intermediate point with the following diagram, moving only north or east at each corner.
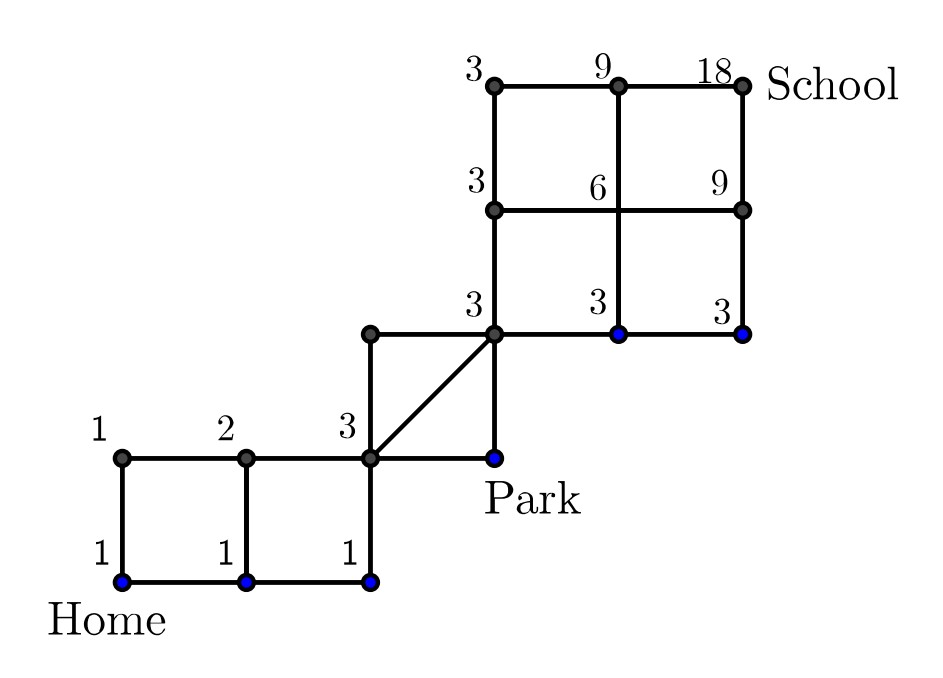
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions