Problem:
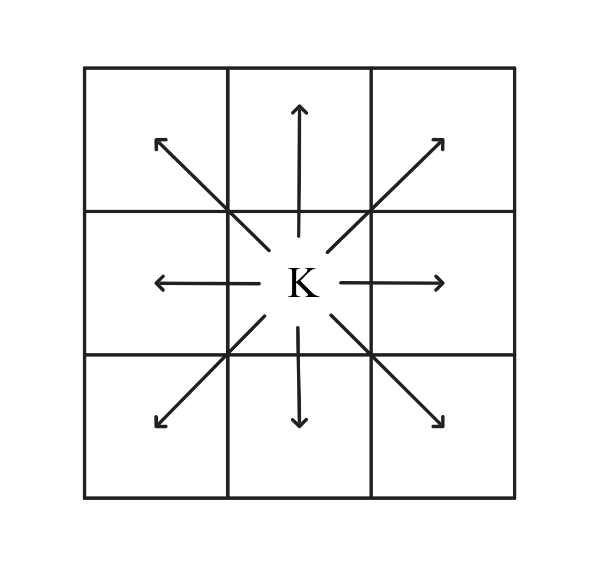
A chess king is said to attack all the squares one step away from it, horizontally, vertically, or diagonally. For instance, a king on the center square of a grid attacks all other squares, as shown below. Suppose a white king and a black king are placed on different squares of a grid so that they do not attack each other. In how many ways can this be done?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Firstly, we note that a king cannot be on the center square as it will attack any other piece on the grid. To solve this problem, we can simply consider some possible cases: one where a king is in the corner and another when one king is on an edge (but not a corner). When one king is placed in any corner, then the other king can be placed in other squares without them attacking each other.
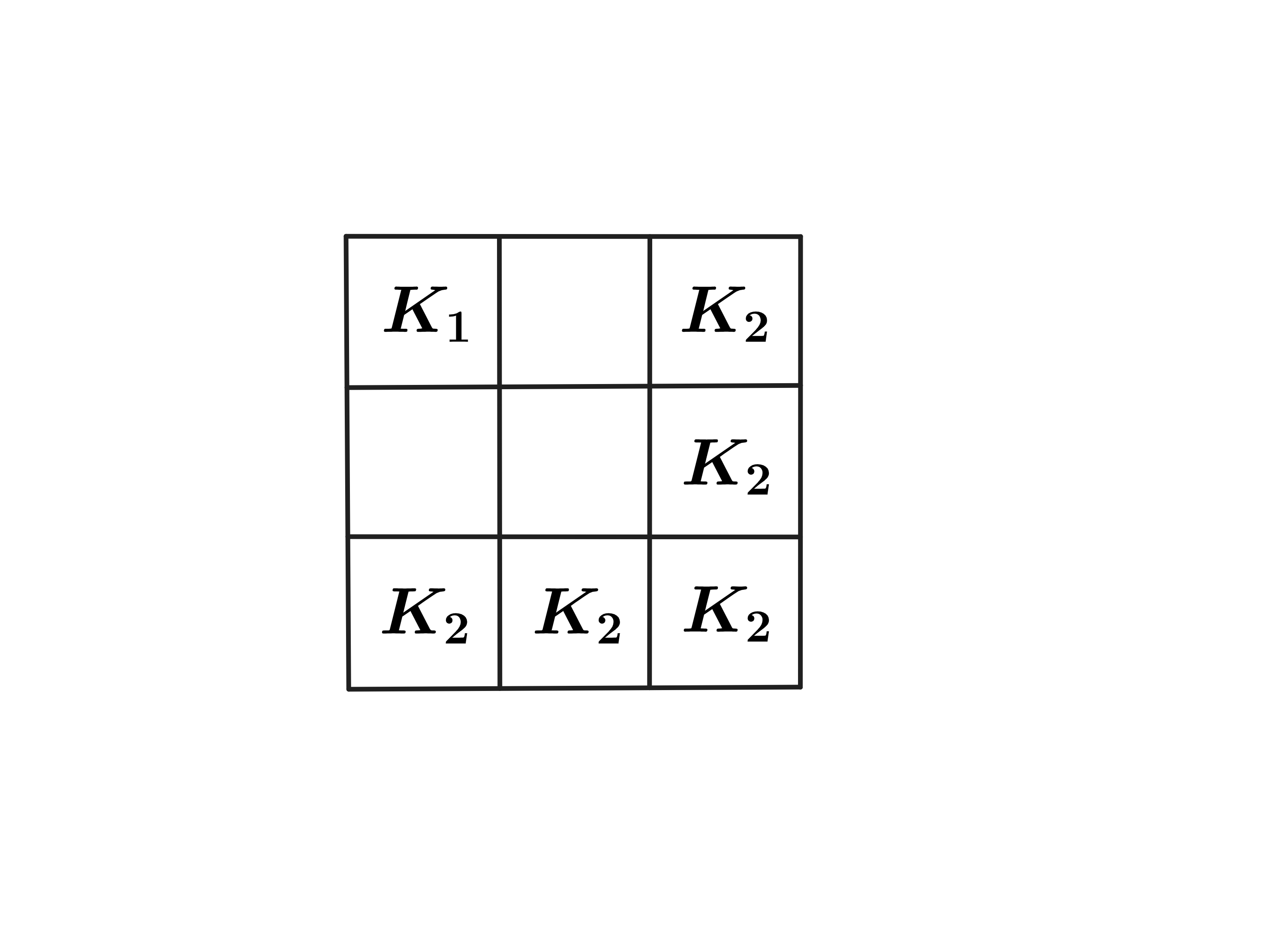
Since there are four corners, we have possibilities for this case. Another possible case is when one king is on an edge that is not a corner.
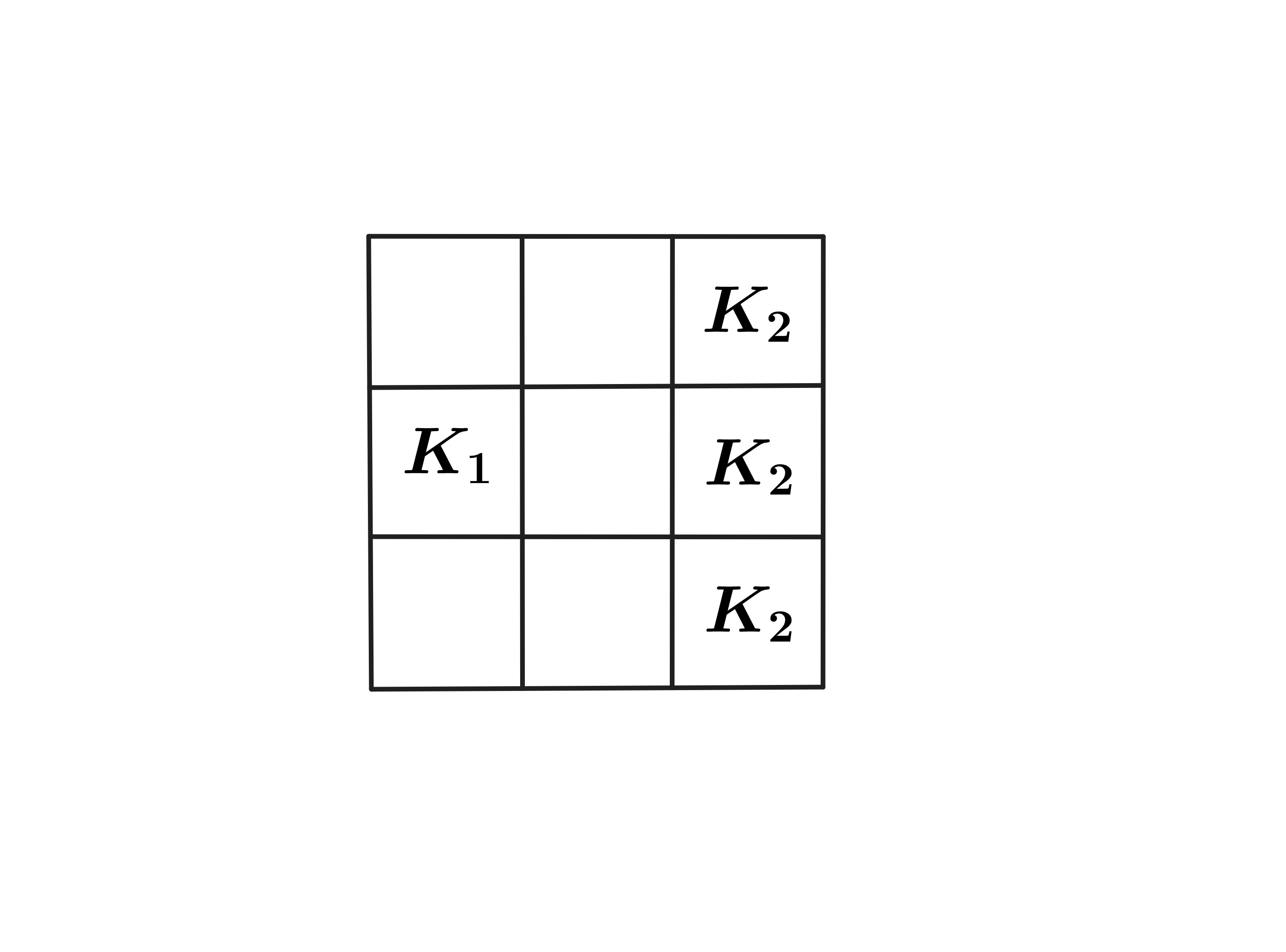
In this scenario, the other king can be in other squares without the two kings attacking each other. There are edges in the grid, so we have possibilities for this case. Adding the number of possibilities, we get total number of ways.
Thus, is the correct answer.
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions