Problem:
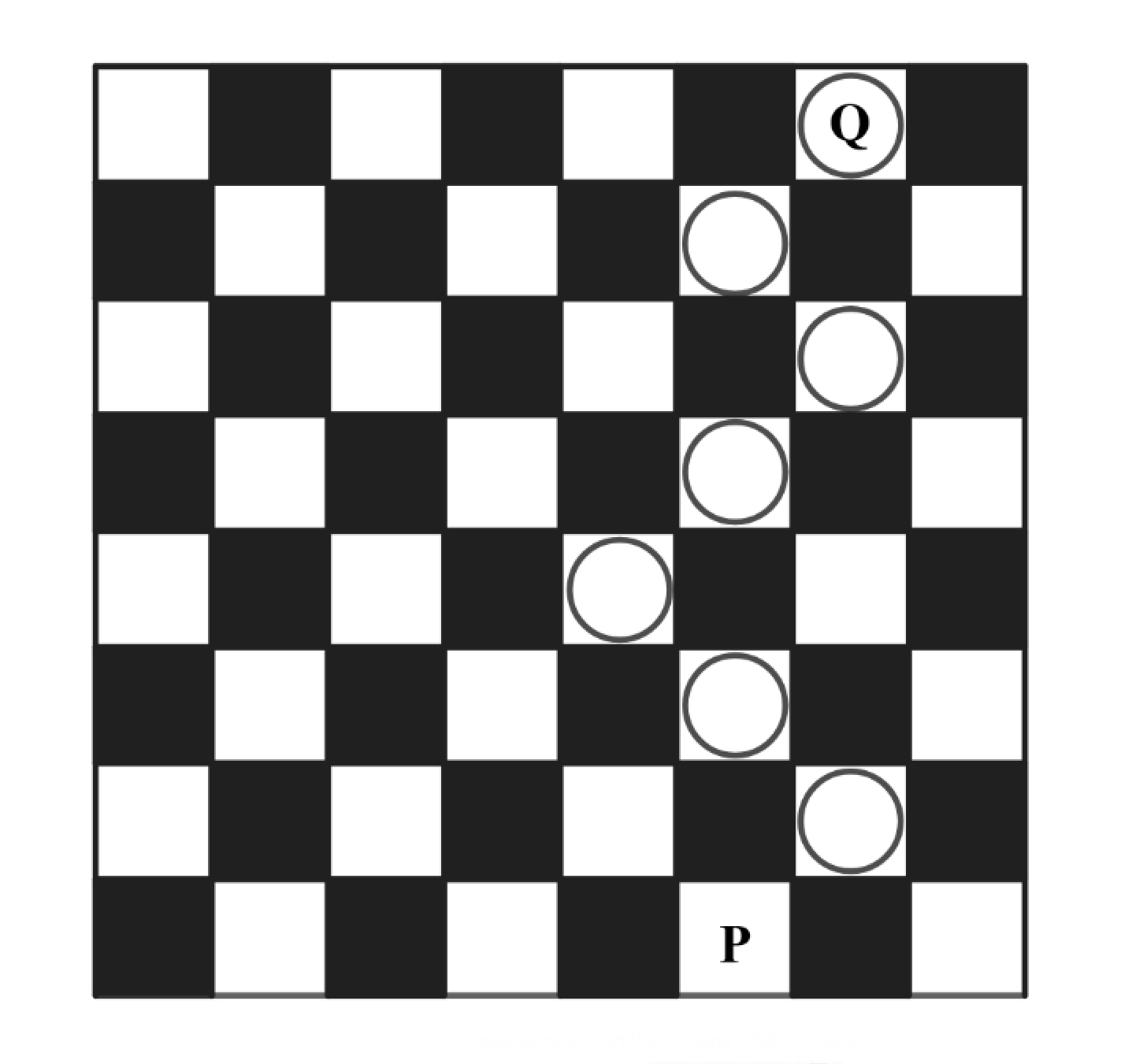
A game board consists of squares that alternate between blank and colored. The figure below shows square in the bottom row and square in the top row. A marker is placed at . A step consists of moving the marker onto one of the adjoining blank squares in the row above. How many -step paths are there from to
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Every move must go either down or up and either left or right. Since the final position is moves up and we move times, every move must go up. Since after moves, we are on the -th row, we can use the -th row to construct the ways to get to each position from the previous moves. Each move can come from the down-left or down-right direction, so we get the ways to get to a point by adding the number of paths from those two directions.

We have then constructed the ways to get to each point from , assuming we always go up. The circled point is , so we have ways to get to . Thus, the correct answer is .
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions